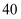七年级(初一)数学下学期下册试题
已知A= -
-
 -
-
-
(1) 化简A
-
(2) 当x满足不等式组
 ,且x为整数时,求A的值.
,且x为整数时,求A的值.
在四个数π、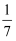 、0、-1中,是无理数的( )
、0、-1中,是无理数的( )
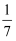 、0、-1中,是无理数的( )
、0、-1中,是无理数的( )
A . π
B . 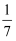 C . 0
D . -1
C . 0
D . -1
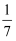 C . 0
D . -1
C . 0
D . -1
已知关于x的不等式  的解集如图所示则a的值为.
的解集如图所示则a的值为.
 的解集如图所示则a的值为.
的解集如图所示则a的值为. 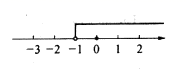
﹣8的立方根是( )
A . 2
B . ﹣2
C . ﹣4
D . 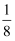
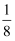
如图,三角形AOB中,A,B两点的坐标分别为(2,4),(6,2).

-
(1) 将线段AB先向左平移m个单位长度再向下平移n个单位长度,得到对应线段CD(点A与点C对应,点B和点D对应),使得点C在x轴上,并且点D在y轴上.
①画出线段CD;
②直接写出线段AB在两次平移过程中扫过的总面积;
-
(2) 若三角形AOB外的点P,满足:三角形AOP、三角形ABP和三角形BOP的面积都相等则点P的坐标可能为.
要反映长沙市一周内每天的最高气温的变化情况,宜采用( )
A . 条形统计图
B . 扇形统计图
C . 折线统计图
D . 频数分布直方图
在太阳系八大行星中,地球与火星是相邻的两颗行星,它们之间的距离约为55 000 000公里,其中数据55 000 000用科学记数法表示为( )
A . 0.55×108
B . 5.5×107
C . 55×106
D . 5.5×106
按照如图所示的程序计算:
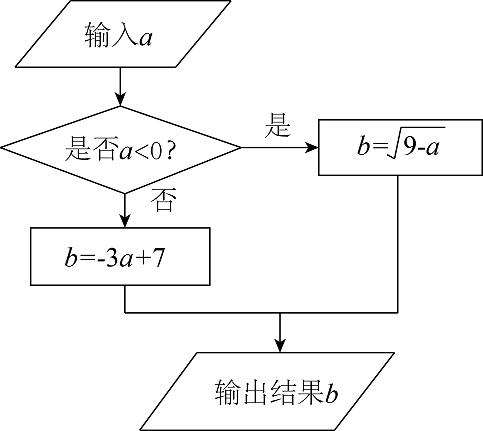
-
(1) 若输入a=﹣9时,求输出结果b的值;
-
(2) 当输入一个正数a时,输出的结果b不大于﹣11,求输入a的取值范围.
解不等式组: 

如图,直线a与∠AOB的一边射线OA相交,∠1=130°,向下平移直线a得到直线b,与∠AOB的另一边射线OB相交,则∠2+∠3=.

铺设木地板时,每两块地板之间的缝隙不低于0.5mm且不超过0.8mm,缝隙的宽度可以是( )
A . 0.3 mm
B . 0.4 mm
C . 0.6 mm
D . 0.9 mm
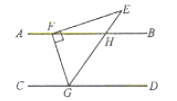
如图,  的顶点
的顶点  分别落在直线
分别落在直线  上,
上,  平分
平分  交
交  于点H,
于点H,  ,
,  .
.
 的顶点
的顶点  分别落在直线
分别落在直线  上,
上,  平分
平分  交
交  于点H,
于点H,  ,
,  .
. 
-
(1) 求
 的度数;
的度数;
-
(2)
 与
与  平行吗?请说明理由.
平行吗?请说明理由.
-
(1)
 ;
;
-
(2)
 .
.
如图,已知AB⊥CD,垂足为O,EF为过点O的一条直线,且∠1=60°,则∠2=( )

A . 70°
B . 30°
C . 40°
D . 120°
有若干个数据,最大值是58,最小值是26,用频数分布表描述这组数据时,若取组距为4,则应分为( )
A . 6组
B . 7组
C . 8组
D . 9组
下列说法中,正确的是( )
①  ;②
;②  一定是正数;③无理数一定是无限小数;④
一定是正数;③无理数一定是无限小数;④  万精确到十分位;⑤
万精确到十分位;⑤  的算术平方根为
的算术平方根为  .
.
A . ①②③
B . ④⑤
C . ②④
D . ③⑤
下列各题估算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.
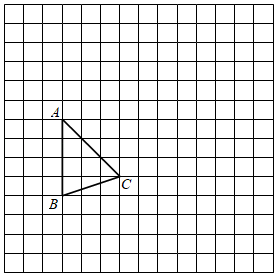
( 1 )将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A'B'C',画出平移后△A'B'C';
( 2 )建立适当的平面直角坐标系,使得点A的坐为(﹣4,3);
( 3 )在(2)的条件下,直接写出点B'的坐标.
阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数x、y满足  ①,
①,  ②,求
②,求  和
和  的值.
的值.
本题常规思路是将①②两式联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①  ②可得
②可得  ,由①
,由①  ②
②  可得
可得  .这样的解题思想就是通常所说的“整体思想”.
.这样的解题思想就是通常所说的“整体思想”.
解决问题:
-
(1) 已知二元一次方程组
 ,则
,则  ,
,  ;
;
-
(2) 某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
-
(3) 对于实数x、y,定义新运算:
 ,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知
,其中a、b、c是常数,等式右边是通常的加法和乘法运算.已知  ,
,  ,那么
,那么  .
.
某文具商店计划用不超过  元的资金购买书包和计算器共
元的资金购买书包和计算器共 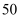 个,已知书包和计算器的进价与售价如表.设购买书包
个,已知书包和计算器的进价与售价如表.设购买书包  个(其中
个(其中  ),购买书包的费用为
),购买书包的费用为  元,购买计算器的费用为
元,购买计算器的费用为  元.
元.
 元的资金购买书包和计算器共
元的资金购买书包和计算器共 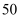 个,已知书包和计算器的进价与售价如表.设购买书包
个,已知书包和计算器的进价与售价如表.设购买书包  个(其中
个(其中  ),购买书包的费用为
),购买书包的费用为  元,购买计算器的费用为
元,购买计算器的费用为  元.
元. | 每件商品 | 进价(元) | 售价(元) |
| 书包 | | |
| 计算器 | | |
-
(1) 当
 时,
时,  ,
,  ;
;
-
(2) 求最多能购买多少个书包;
-
(3) 设售出这批书包和计算器共盈利
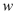 元,求
元,求 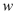 与
与  之间的函数关系式;文具店购进多少个书包时,才能获得最大利润?最大利润是多少?
之间的函数关系式;文具店购进多少个书包时,才能获得最大利润?最大利润是多少?
最近更新
- 2009年8月我国台湾省遭受强台湾“莫拉克”袭击,造成巨大的财产损失和人员伤亡,结合图6,回答下面试题 9.此次台湾重灾
- 计算
- ---Ihave to be off right now. ---Whata pity!I______ you coul
- 在等差数列{an}中,若S12=8S4,则等于A. B.
- 2013年深化经济体制改革重点工作开展以来,国务院和发改委已取消和下放149项行政审批事项,这表明 A.政府管理的职能应
- (08年执信中学期中物理文)(6分)在奥斯特发现电流的磁效应之后,法国的物理学家 第一个做了通电平行导线
- 同时具有以下性质: “①最小正周期是; ②图像关于直线对称; ③ 在上是增函数”的一个函数是
- 天平标尺上的分度值是0.2g,最大示数是5g。调好后,左盘放入被测物体,右盘放入一个5g的砝码,横梁指针指在分度盘中线的
- 下列叙述正确的是
- -- _________ do you have a computer class,Daming and Betty?
- 下列叙述中正确的是 A.布朗运动就是液体分子的无规则运动B.当分子力表现为引力时,分子势能随分子间距离的增加而增加C.
- 6.春秋时期,井田制瓦解的根本原因是: A、私田增多 B、铁器牛耕的使用推动了生产力的发 C
- 牙膏是人们生活的必需品,在牙膏生产过程中需加一种摩擦剂,这种摩擦剂是由一种矿石经下列变化制得的极细的粉末。 则该矿
- If I you, I would go to the party. A.was
- 常温下,甲溶液中水电离出的H+浓度为10-12 mol/L,乙溶液中水电离出的H+浓度为 10-2mol/L,下列说法正
- The world is not coming to an end on December 21, 2012, the
- 在下面这段话中,顺序排列最恰当的一项是( )(2分)保护动物已不是人们陌生的话题。人类的发展,也早已达到可以
- 维生素C主要存在于蔬菜、水果中,它能增强人体对疾病的抵抗能力。①取3片维生素C压碎后溶于10mL水中过滤,取少量滤液向其
- 当今,中国的对外开放正向纵深领域发展。中国对外开放的每一步都意味着对 海洋的挺进,大国崛起必须经略海洋已成共识。从
- 有关NaHCO3和Na2CO3的性质,以下叙述错误的是( ) A.等质量的NaHCO3和Na2CO3与足量盐酸反应