七年级(初一)数学下学期下册试题
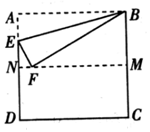
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE。若AB的长为2,则FM的长为。
不等式组  的解集是.
的解集是.
 的解集是.
的解集是.
如图(1)所示,同位角共有( )
A . 1对
B . 2对
C . 3对
D . 4对
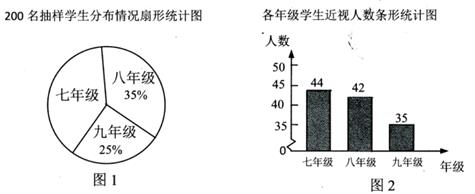
我国青少年视力情况已经受到全社会的广泛关注.某校随机调研了200名初中七八九年级学生的视力情况,并把调查数据绘制成如下不完整统计图:
-
(1) 七年级参与调查的有多少人?若该校有七年级学生400人,请估计七年级近视人数;
-
(2) 某同学说“由图2可知,从七年级到九年级,近视率越来越低”,你认为这个说法正确吗?请作出判断,并说明理由。
满足﹣1<x≤2的数在数轴上表示为( )
A .  B .
B .  C .
C .  D .
D . 
不等式组﹣1+a<2x﹣1<b的解集为 <x<
<x<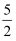 , 则a﹣b=
, 则a﹣b=
 <x<
<x<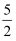 , 则a﹣b=
, 则a﹣b=
规定一种运算:a*b= 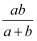 ;计算2*(﹣3)的值是.
;计算2*(﹣3)的值是.
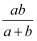 ;计算2*(﹣3)的值是.
;计算2*(﹣3)的值是.
实数a,b在数轴上的位置如图所示,则  =.
=.
 =.
=. ![]()
已知432=1849,442=1936,452=2025,462=2116,若n为整数,且n< <n+1,则n的值为 .
<n+1,则n的值为 .
 <n+1,则n的值为 .
<n+1,则n的值为 .
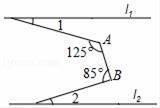
如图,直线l1∥l2 , ∠A=125°,∠B=85°,则∠1+∠2=.
下面几个数:3.14,  ,
,  ,
, 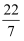 ,
,  ,其中,无理数的个数有( )
,其中,无理数的个数有( )
 ,
,  ,
, 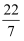 ,
,  ,其中,无理数的个数有( )
,其中,无理数的个数有( )
A . 1
B . 2
C . 3
D . 4
(阅读材料)
在进行计算或化简时,可以根据题目特点,将一个分数或分式变成两部分之差,如: 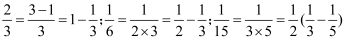 等.
等.
(问题解决)
利用上述材料中的方法,解决下列问题:
-
(1) 求
 的值;
的值;
-
(2) 求
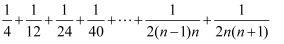 的值;
的值;
-
(3) 求
 的值.
的值.
为支持地方,大庆市萨尔图区、让胡路区、红岗区三地现分别有物资100吨、100吨、80吨,需全部运往肇东和肇源两地,根据需要情况,这批物资运往肇东的数量比运往肇源的数量的2倍少20吨.
-
(1) 求这赈灾物资运往肇东和肇源的数量各是多少?
-
(2) 若要求红岗区运往肇东的物资为60吨,萨尔图区地运往肇东的物资为x吨(x为整数),让胡路区运往肇东的物资数量小于萨尔图区地运往肇东的物资数量的2倍,其余的物资全部运往肇源,且让胡路区运往肇源的物资数量不超过25吨,则萨尔图区、让胡路区两地的物资运往肇东和肇源的方案有几种?
-
(3) 已知萨尔图区、让胡路区、红岗区三地的物资运往肇东和肇源的费用如表:
萨尔图区
让葫芦区
红岗区
运往肇东的费用(元/吨)
220
200
200
运往肇源的费用(元/吨)
250
220
210
为即时将这批物资运往肇东和肇源,某公司主动承担运送这批物资的总费用,在(2)问的要求下,该公司承担运送这批物资的总费用最多是多少?
某服装厂生产一种西装和领带,西装每套定价400元,领带每条定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案①:买一套西装送一条领带;
方案②:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20)
-
(1) 若该客户按方案①购买,需付款元(用含x的代数式表示);
若该客户按方案②购买,需付款元(用含x的代数式表示);
-
(2) 若x=30,通过计算说明此时按哪种方案购买较为合算?
-
(3) 若两种优惠方案可同时使用,当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算出此种方案的付款金额.
多项式y2-my+144成为完全平方式,则m的值为( )
A . 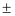 12
B . 24
C . ±24
D . 12
12
B . 24
C . ±24
D . 12
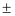 12
B . 24
C . ±24
D . 12
12
B . 24
C . ±24
D . 12
若  ,
,  .
.
 ,
,  .
.
-
(1) 求
 的值;
的值;
-
(2) 若
 的小数部分为
的小数部分为  ,
,  的小数部分为
的小数部分为  ,求
,求 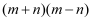 的值.
的值.
实数a,b在数轴上的位置如图所示,则|a|﹣|b|可化简为( )
![]()
A . a﹣b
B . b﹣a
C . a+b
D . ﹣a﹣b
解不等式组并写出不等式组的整数解.
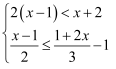
如图,∠1=105°,∠2=140°,那么∠3=( )

A . 55°
B . 65°
C . 75°
D . 85°
-
(1) 计算:20180﹣(
 )﹣1+
)﹣1+ 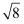 .
.
-
(2) 化简:
 .
.
最近更新
- 如下图所示的甲、乙两个装置中,胶头滴管中吸入某种液体,平底烧瓶中放入另一种物质,挤压胶头滴管加入液体,一段时间后甲装置中
- The project ______ by the end of 2011 will expand the city’s
- 下列词语中,没有错别字的一项是 ( ) (3分)
- 如图所示是小明探究“比较水和煤油的比热容大小”的实验装置。 (1)为保证让水和煤油在相同时间内能吸收相同的热量,甲、
- 某含苯环的烃A,其相对分子质量为104,碳的质量分数为92.3%。(1)A的分子式为
- 下列词语中加点的字,每对读音都不相同的一组是( ) A.松柏/柏油攒射/万头攒动数见不
- 下列叙述中属于化学变化的是 A.舞台上用干冰制造云雾 B.浓盐酸挥发,形成白雾 C
- 【甲】治水必躬亲 治水之法,既不可执一,泥于掌故,亦不可妄意轻信人言。盖地
- 数列满足: 证明:(1)对任意为正整数;(2)对任意为完全平方数。
- 光线从折射率为的媒质中射向空气,如果入射角为60°,则图19-3-8所示光路中可能的是( )图19-3-8
- 做化学实验必须注意安全,下列属于安全操作的是 ( ) A、加热试
- 一对平行金属板水平放置,板间距离为d,板间有磁感应强度为B的水平向里的匀强磁场,将金属板连入如图所示的电路,已知电源内阻
- 17. 下面是中国青年志愿者协会的标志,请从图案设计的角度揭示这个图形的构图要素和寓意,要求语意简明,句子通顺,不超过8
- We would like you ________ and we look forward _________ you
- 某地曾是著名的鱼米之乡,植物生长茂盛,土壤动物种类繁多。后来,由于上游地区一农药厂的污染废水排入河流,造成该地农田土壤环
- 下列叙述肯定能说明金属A比金属B的活泼性强的是( )A.A原子的最外层电子数比B原子的最外层电子数少B.A原子的电
- 关于油脂在人体中的生理功能的理解中错误的是 A.油脂在人体内的水解、氧化可释放能量,所以油脂可在人体内提供能量 B.为人
- 观察下图: 1 2 3 4 3 4 5 6 7 4 5 6 7 8 9 10 ………… 则第( )行
- 在有丝分裂过程中,不属于着丝点分裂的结果是 A.染色单体消失



