七年级(初一)数学下学期下册试题
已知关于x、y的二元一次方程组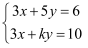 给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )
给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )
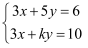 给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )
给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )
A . ①②③
B . ①③
C . ②③
D . ①②
如图所示,下列推理不正确的是( )

A . 若∠AEB=∠C,则AE∥CD
B . 若∠AEB=∠ADE,则AD∥BC
C . 若∠C+∠ADC=180°,则AD∥BC
D . 若∠AED=∠BAE,则AB∥DE
如图,AB∥CD,∠AFE=α,∠DCE=β,则∠E为( )
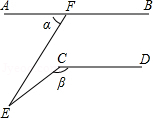
A . β﹣α
B . α+β﹣180°
C . β﹣2α
D . 180°﹣α﹣β
解下列方程或方程组:
①2(x﹣2)﹣3(4x﹣1)=9(1﹣x);
②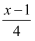 =
=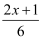 ;
;
③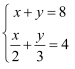 ;
;
④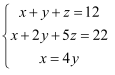 .
.
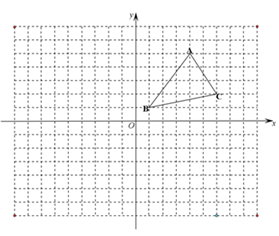
如图,在边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,△ABC的三个顶点都在网格的格点上.
-
(1) 把△ABC向下平移6个单位长度,再向左平移5个单位长度,得到△A1B1C1.请直接写出点A1、点B1和点C1的坐标.(不需要画图)
-
(2) 求△ABC的面积.
-
(3) 点D的坐标为(-3,1),在坐标轴上是否存在点E使得△BDE的面积等于△ABC的面积,若存在,请直接写出点E的坐标,若不存在,请说明理由.
为了让市民享受到更多的优惠,某市针对乘坐地铁的人群进行了调查.
-
(1) 为获得乘坐地铁人群的月均花费信息,下列调查方式中比较合理是 ;A . 对某小区的住户进行问卷调查 B . 对某班的全体同学进行问卷调查 C . 在市里的不同地铁站,对进出地铁的人进行问卷调查
-
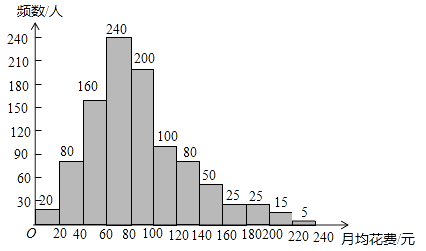
(2) 调查小组随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了
频数分布直方图,如图所示.
① 根据图中信息,估计平均每人乘坐地铁的月均花费的范围是元;
A.20—60 B.60—120 C.120—180
②你是用(填统计概念)对①进行估计的。
③为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.根据图中信息,乘坐地铁的月均花费达到元的人可以享受扣.
下列不等式变形正确的是( )
A . 由a>b得ac>bc
B . 由a>b得﹣2a>﹣2b
C . 由a>b得﹣a<﹣b
D . 由a>b得a﹣2<b﹣2
先化简,再求值: 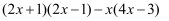 ,其中x=-2.
,其中x=-2.
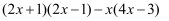 ,其中x=-2.
,其中x=-2.
如图,在平面直角坐标系  中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形
中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形 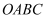 的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
 中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形
中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形 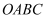 的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动). 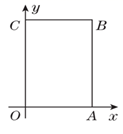
-
(1) 点B的坐标为;
-
(2) 当点P移动4s时,求出点P的坐标;
-
(3) 在移动过程中,当点P到
 轴的距离为5个单位长度时,求点P移动的时间t .
轴的距离为5个单位长度时,求点P移动的时间t .
计算: 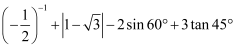
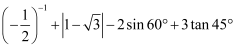
若不等式ax|a-1|>2是一元一次不等式,则a=.
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是

已知抛物线y1=a(x﹣m)2+k与y2=a(x+m)2+k(m≠0)关于y轴对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=﹣4x2+6x+7的“和谐抛物线”.
大家都知道,九点五十五分可以说成十点差五分.这启发人们设计了一种新的加减记数法.比如:9写成 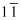 ,
, 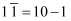 ,198写成
,198写成  ,
, 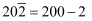 ;7683写成
;7683写成 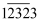 ,
, 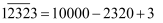 ,…总之,数字上画一杠表示减去它,按这个方法请计算:
,…总之,数字上画一杠表示减去它,按这个方法请计算: 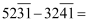 ( )
( )
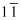 ,
, 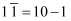 ,198写成
,198写成  ,
, 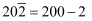 ;7683写成
;7683写成 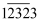 ,
, 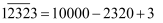 ,…总之,数字上画一杠表示减去它,按这个方法请计算:
,…总之,数字上画一杠表示减去它,按这个方法请计算: 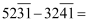 ( )
( )
A . 2010
B . 2019
C . 2020
D . 2021
在平面直角坐标系中,已知线段  的两个端点分别是
的两个端点分别是  ,将线段
,将线段  平移后得到线段
平移后得到线段 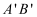 ,若点
,若点 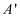 的坐标为
的坐标为  ,则点
,则点 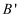 的坐标为( )
的坐标为( )
 的两个端点分别是
的两个端点分别是  ,将线段
,将线段  平移后得到线段
平移后得到线段 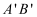 ,若点
,若点 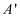 的坐标为
的坐标为  ,则点
,则点 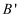 的坐标为( )
的坐标为( )
A .  B .
B . 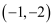 C .
C . 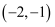 D .
D . 
 B .
B . 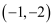 C .
C . 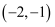 D .
D . 
一个正数的平方根是3a-2与4-a,则这个正数是.
下列命题是真命题的是( )
A . 如果两个角不相等,那么这两个角不是对顶角
B . 两互补的角一定是邻补角
C . 如果a2=b2 , 那么a=b
D . 如果两角是同位角,那么这两角一定相等
解不等式组 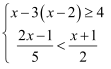 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.
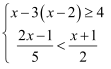 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.
在实数0,  ,﹣3.14,0.1010010001…(每两个1之间的0的个数依次增加1),
,﹣3.14,0.1010010001…(每两个1之间的0的个数依次增加1),  ,
,  ,无理数有个,有理数有个,负数有个.
,无理数有个,有理数有个,负数有个.
 ,﹣3.14,0.1010010001…(每两个1之间的0的个数依次增加1),
,﹣3.14,0.1010010001…(每两个1之间的0的个数依次增加1),  ,
,  ,无理数有个,有理数有个,负数有个.
,无理数有个,有理数有个,负数有个.
不等式组  的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A . x≤4
B . 2<x≤4
C . 2≤x≤4
D . x>2
最近更新
- 如图所示,直角坐标系位于竖直平面内,x轴水平,一长为2L的细绳一端系一小球,另一端固定在y轴上的A点,A点坐标为(0,L
- We pursue happiness,thinking oneday we will find it.But ____
- (2010浙江温州30)检测发现许多蔬菜中含有亚硝酸盐,当亚硝酸盐达到一定量时,会对人体产生危害。生活中,蔬菜有室温贮存
- 将SO2气体通入BaCl2溶液中,未见白色沉淀,继续通入另一种气体立即产生沉淀,则通入的气体不可能的是 A.Cl2
- 麦角醇(ergosterol)在紫外光照射下可转化为抗软骨病的维生素D2,麦角醇的结构为:下列关于该化合物的说法正确的是
- 仅改变下列一个条件,通过提高活化分子的百分率来提高反应速率的是 ( )A.加热 B
- It is the first time ____ I have come to your city.A. that
- 2007年3月27日,北京奥组委发布了北京2008年奥运会奖牌式样。下面介绍奖牌的句子,合理的排序应该是
- 下列各项最能说明鸦片战争爆发的历史必然性的是( )A.清王朝奉行闭关锁国政策 B.中国落后
- 完形填空 阅读下面短文,掌握其大意,然后从41---55各题所给的A、B、C、D四各选项中,选出一个最佳答案。
- 当打开一个装有液态空气的容器盖,并将一根燃着的木条置于容器口上方,观察到的现象是( ) a.燃烧得更旺
- 函数在区间内的零点个数是 (A)0 (B)1 (C)2 (D)3
- 下列各诗句中,运用通感艺术手法的一项是( ) A.桃红复含宿雨,柳绿更带朝烟。花落家童未扫,莺啼山客犹眠。 B.凤
- ____ at a college or university in the USA, Chinese and othe
- 在水平地面上有一质量为5 kg的物体,它受到与水平方向成53°斜向上的25 N的拉力时,恰好做匀速直线运动,取g=10
- As we know, in our Chinese history _____ was a time when ind
- 某蛋白质由n条肽链组成,氨基酸的平均相对分子质量为a,若在缩合过程中失去的水的总相对分子质量为b,则该蛋白质是由多少个氨
- 阳光穿过森林中的空隙形成“光斑”,它会随太阳的运动和枝叶的摆动而移动。下图表示一株生长旺盛的植物在“光斑”照射前后的光合
- 已知x,y∈R,若x2+2x+(2y+x)i和3x-(y+1)i是共轭复数,求复数z=x+yi和.
- 关于功率,下列各种说法正确的是()A、功率大说明物体做的功多B、功率小说明物体做功慢C、由P=W/t可知机器做功越多,其



