七年级(初一)数学下学期下册试题
不等式组  的解集为.
的解集为.
 的解集为.
的解集为.
在对某一地区的一次人口抽样统计分析中,各年龄段(年龄为整数)人数如下表所示:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
请根据此表回答下列问题:
-
(1) 这次抽样的样本容量是;
-
(2) 如果该地区现有人口8000人,为关注人口老龄化问题,请估计该地区60岁以上(含60岁)的人口数为.
如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( )

A . 60°
B . 80°
C . 120°
D . 150°
估计  的值应在( )
的值应在( )
 的值应在( )
的值应在( )
A . 3和4之间
B . 4和5之间
C . 5和6之间
D . 6和7之间
如图, 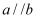 ,若
,若  ,则
,则  的度数是( )
的度数是( )
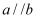 ,若
,若  ,则
,则  的度数是( )
的度数是( ) 
A .  B .
B . 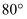 C .
C .  D .
D . 
 B .
B . 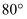 C .
C .  D .
D . 
解不等式组 

请结合题意填空,完成本题的解答:
-
(1) 解不等式(1),得.
-
(2) 解不等式(2),得.
-
(3) 把不等式(1)和(2)的解集在数轴上表示出来

-
(4) ∴原不等式组的解集为.
用四个不等式①a>b,②ab>b2 , ③a>0,④b>0中的两个不等式作为题设,余下的两个不等式中选择一个作为结论,组成一个真命题:.
估算:  ≈(误差小于1).
≈(误差小于1).
 ≈(误差小于1).
≈(误差小于1).
中国的数字支付正在引领未来世界的支付方式变革。某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

|
|

-
(1) 这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;
-
(2) 将条形统计图补充完整 .观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是;
-
(3) 在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表的方法,求两人选同种支付方式的概率.
如图,直线l1∥l2 , AB⊥CD,∠1=35°,那么∠2的度数是.

如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )

A . BM+CN=MN
B . BM﹣CN=MN
C . CN﹣BM=MN
D . BM﹣CN=2MN
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )

A . ∠3=∠4
B . ∠D+∠ACD=180°
C . ∠D=∠DCE
D . ∠1=∠2
下列事件中,是必然事件的是( )
A . 通常加热到100°C时,水沸腾
B . 掷一次骰子,向上一面的点数是6
C . 经过有交通信号灯的路口,遇到红灯
D . 射击运动员射击次,命中靶心
已知点  在
在  轴上,则点
轴上,则点  的坐标是( )
的坐标是( )
 在
在  轴上,则点
轴上,则点  的坐标是( )
的坐标是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.

-
(1) 根据如图,分别求出两班复赛的平均成绩和方差;
-
(2) 根据(1)的计算结果,分析哪个班级5名选手的复赛成绩波动小?
已知如图, ,
,  ,
,  ,
,  , 求证:
, 求证: .
.
 ,
,  ,
,  ,
,  , 求证:
, 求证: .
. 完成下面的证明过程:

证明:∵ ,
,
∴ ( )
( )
∵ ▲ (已知)
∴ .( )
.( )
∴ .
.
∵ , (已知)
, (已知)
∴ ▲
▲
又∵ ,
,
∴ ,
,
∴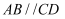 , ( )
, ( )
∴ .( )
.( )
如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A=度.

点P(﹣5,1)到x轴距离为.
某校有500名学生.为了解全校每名学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到扇形统计图如右图:

-
(1) 本次调查的个体是,样本容量是;
-
(2) 扇形统计图中,乘私家车部分对应的圆心角是度;
-
(3) 请估计该校500名学生中,选择骑车和步行上学的一共有多少人?
如图,以点C(0,1)为位似中心,将△ABC按相似比1:2缩小,得到△DEC,则点A(1,﹣1)的对应点D的坐标为.

最近更新
- 阅读下面的文字,完成后面的问题。 60年来中国为何不出文学大师? 黄 麟 上世纪三、四十年代,中国出了鲁迅等一批文学
- 已知函数. (1)若,求函数在上的单调增区间; (2)若函数在区间上是单调递减函数,求实数的取值范围.
- 下列A、B实验操作中,请将必须先做的操作编号(A、B)填在答案栏中。实验项目操作A操作B答案用排水法收集氧气完毕后把导管
- —I wonder whether they have enough books for each of us. —
- 为使显微镜视野右下方的细胞移到视野的正中央,应把装片向哪个方向移动( )A.右下方B.右上方C.左上方D.左下方
- 下列各句加点的成语,使用恰当的一句是 A.股票交易中心的门前人潮如涌,侯门似海,想挤进去,还确实费劲。 B.不论什么
- (6分)400K 101.3kPa时,1.5L某烃蒸气能在aL氧气中完全燃烧,体积增大至(a+3)L (同温同压下测定)
- — Is it OK if I take this seat? —Sorry,___________. A. here
- 正电子(PET)发射计算机断层显像的基本原理是:将放射性同位素注入人体,参与人体的代谢过程。在人体内衰变放出正电子,与人
- (08年遵义四中期中)下列说法正确的是A.布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映B.没有摩擦的理想热机可以
- .When_________different cultures, we often pay attention onl
- 下图甲、乙表示真核生物遗传信息传递过程中的某两个阶段的示意图,图丙为图乙中部分片段的放大示意图。对此分析合理的是A.图甲
- 20世纪50年代是中国人在夺取全国政权以后,开始按照自己的理想建设全新的社会政治制度的第一个阶段。下列关于1955年我国
- 抗虫棉植株的变异来源及大面积推广种植所采用的技术手段分别是 ①基因突变 ②基因重组 ③染色体变
- 在17-18世纪的启蒙运动中,他激烈抨击天主教教会的罪恶行径,把教士称作“文明的恶棍”,骂教皇是“两足禽兽”。他是 A.
- 下列各组词语中加点字的读音,全都正确的一组是 () A.削减(xuē) 桎梏(gù)
- At the graduation c , the headmaster gave us an im
- 李响利用电压表和电流表测量小灯泡的电功率。(1)(2分)请用笔画线代替导线把图24所示的实验电路连接完整(连线时导线不得
- 下列关于细胞分化、衰老、凋亡和癌变的叙述正确的是( ) A.衰老的生物体中,细胞都处于衰老状态 B.被病原体感染的
- . Some animals are in danger, and the scientists are doing _



