七年级(初一)数学下学期下册试题
红树林中学共有学生1600人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了200名学生,其中有60名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有人.
已知,△ABC 在直角坐标系内,三个顶点的坐标分别为 A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

( 1 )画出△ABC向下平移4个单位得到的△ 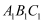 ;
;
( 2 )以点B为位似中心,在网格内画出△  ,使△
,使△  与△ABC 位似,且位似比为 2:1;
与△ABC 位似,且位似比为 2:1;
( 3 )△  与△
与△ 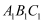 是位似图形,位似中心为原点,位似比为 3:2,若 M(a, b)为线段
是位似图形,位似中心为原点,位似比为 3:2,若 M(a, b)为线段  上任一点,写出点 M 对应点
上任一点,写出点 M 对应点 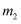 的坐标.
的坐标.
为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成两幅不完整的统计图如图所示,则抽查的学生中户外活动时间为1.5小时的人数 .

我们定义一种新运算a⊕b=  ,例如5⊕2=
,例如5⊕2=  ,则式子7⊕(﹣3)的值为( )
,则式子7⊕(﹣3)的值为( )
 ,例如5⊕2=
,例如5⊕2=  ,则式子7⊕(﹣3)的值为( )
,则式子7⊕(﹣3)的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形) 的顶点A,C的坐标分别为
的顶点A,C的坐标分别为
 的顶点A,C的坐标分别为
的顶点A,C的坐标分别为

-
(1) 请在网络平面内做出平面直角坐标系;
-
(2) 将三角形
 平移得三角形
平移得三角形 , 已知
, 已知 , 请在网格中作出三角形
, 请在网格中作出三角形 , 并写出
, 并写出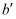 点的坐标: ▲ .
点的坐标: ▲ .
-
(3) 求三角形
 的面积.
的面积.
下列问题中,应采用抽样调查的是( )
A . 企业招聘,对应聘人员进行面试
B . 了解某班学生的身高情况
C . 调查春节联欢晚会的收视率
D . 了解某校七年级第二学期期末考试各班的数学科平均成绩
不等式﹣2x>  的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A . x<﹣  B . x<﹣1
C . x>﹣
B . x<﹣1
C . x>﹣  D . x>﹣1
D . x>﹣1
 B . x<﹣1
C . x>﹣
B . x<﹣1
C . x>﹣  D . x>﹣1
D . x>﹣1
光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图,水面  与水杯下沿
与水杯下沿  平行,光线
平行,光线  从水中射向空气时发生折射,光线变成
从水中射向空气时发生折射,光线变成  ,点G在射线
,点G在射线  上,已知
上,已知  ,求
,求  的度数.
的度数.
 与水杯下沿
与水杯下沿  平行,光线
平行,光线  从水中射向空气时发生折射,光线变成
从水中射向空气时发生折射,光线变成  ,点G在射线
,点G在射线  上,已知
上,已知  ,求
,求  的度数.
的度数. 
如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=cm.

依据不等式的性质,把下列不等式化成x>a或x<a的形式:
-
(1) x+3<5
-
(2) x-
 >
> 
下列命题是假命题的是( )
A . 垂线段最短
B . 内错角相等
C . 在同一平面内,不重合的两条直线只有相交和平行两种位置关系
D . 若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直
有一片牧场原有的草量为  ,草每天都匀速地生长,这片牧场每天牧草的生长量都为
,草每天都匀速地生长,这片牧场每天牧草的生长量都为  .若在其上放牧24头牛,则6天吃完牧草.若放牧21头牛,则8天吃完牧草.若每头牛每天吃草的量也都是相等的,设每头牛每天吃草的量为
.若在其上放牧24头牛,则6天吃完牧草.若放牧21头牛,则8天吃完牧草.若每头牛每天吃草的量也都是相等的,设每头牛每天吃草的量为  .问:
.问:
 ,草每天都匀速地生长,这片牧场每天牧草的生长量都为
,草每天都匀速地生长,这片牧场每天牧草的生长量都为  .若在其上放牧24头牛,则6天吃完牧草.若放牧21头牛,则8天吃完牧草.若每头牛每天吃草的量也都是相等的,设每头牛每天吃草的量为
.若在其上放牧24头牛,则6天吃完牧草.若放牧21头牛,则8天吃完牧草.若每头牛每天吃草的量也都是相等的,设每头牛每天吃草的量为  .问:
.问:
-
(1) 放牧24头牛,6天所吃的牧草量用含
 ,
,  的代数式表示为
的代数式表示为 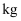 ;放牧21头牛,8天所吃的牧草量用含
;放牧21头牛,8天所吃的牧草量用含  ,
,  的代数式表示为
的代数式表示为 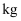 ;
;
-
(2) 试用
 表示
表示  ,
,  ;
;
-
(3) 若放牧16头牛,则几天可以吃完牧草?
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1)

( 1 )将△ABC关于y轴对称得到△A1B1C1 , 画出△A1B1C1 , 并写出点B1的坐标;
( 2 )把△A1B1C1平移,使点B1平移到B2(3,1),请作出△A1B1C1平移后的△A2B2C2 , 并写出A2的坐标;
( 3 )已知△ABC中有一点D(a , b),求△A2B2C2中的对应点D2的坐标.
实数 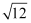 的整数部分是.
的整数部分是.
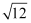 的整数部分是.
的整数部分是.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.

-
(1) 求证:四边形BCED是平行四边形;
-
(2) 已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
为有效推进爱国卫生“7个专项行动”,全面改进学校环境卫生,某校计划购进甲、乙两种新型垃圾桶,调查发现,若购买甲种垃圾桶5个、乙种垃圾桶2个,共需资金1380元;若购买甲种垃圾桶7个、乙种垃圾桶3个,共需资金1980元.
-
(1) 甲、乙两种型号的新型垃圾桶每个的价格各是多少元?
-
(2) 若该校计划购进这两种垃圾桶共28个,其中乙种垃圾桶的数量不少于甲种的数量,学校至多能提供资金6000元,你认为学校有几种购买方案?哪种购买方案所需资金最少?最少资金是多少元?
实数a,b在数轴上对应点的位置如图所示,下列结论正确的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
不等式组  的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A .  B .
B .  C .
C .  D . 无解
D . 无解
 B .
B .  C .
C .  D . 无解
D . 无解
如图,若直线  //
//  ,
,  是截线,∠1 = 32°,则∠3的度数是.
是截线,∠1 = 32°,则∠3的度数是.
 //
//  ,
,  是截线,∠1 = 32°,则∠3的度数是.
是截线,∠1 = 32°,则∠3的度数是. 
解不等式组  ,并写出x的所有整数解.
,并写出x的所有整数解.
 ,并写出x的所有整数解.
,并写出x的所有整数解.
最近更新
- 右图装置可用于气体的收集、检验、除杂和体积的测量等,不能完成的实验是 A.气体从a端通入,收集氧气
- 分式方程的解是.
- 已知,求代数式的值。
- 在“利用自由落体验证机械能守恒定律”的实验中,由于运动的初始阶段计时器打出的一些点子模糊不清,故必须选择比较清楚的点作为
- 如图所示,电源电压U=12V,小灯泡L的额定电压为6V,当滑动变阻器的滑片P移至中点时,小灯泡L正常发光;当滑片P移至最
- My grandfather lives in a village________,but he never feels
- 如图是实验室制取气体的常用装置图:(1)亮亮要制取两瓶二氧化碳,他应选用的制取装置为 ,(填编号,下同),检验所制气体是
- 已知与的夹角为,,,,,且在取得最小值,当时,求的取值范围.
- 在水稻→蝗虫→青蛙 这条食物链中,有人大量捕杀青蛙,水稻产量将会( ) A.减少 B.不变
- 下图所示为甘蔗的叶肉细胞内的系列反应过程,下列有关说法正确的是 ( )A.过程①消耗CO2释放O2,过程③消耗O2释
- 将纯锌片和纯铜片按图所示插入相同浓度的稀硫酸中,以下有关叙述正确的是A.甲装置子中电能转化为化学能 B.乙
- 2014年3月5日,十二届全国人大二次会议在人民大会堂开幕,李克强总理在十二届全国人大二次会议开幕式上指出,2014年继
- —Excuse me, arethere some Chinese works of art exhibit
- .农村由人民公社到家庭联产承包责任制,这一重大改革的变化表现在:( ) ①土地所有制 ②经营管理方法 ③生产经营的权利
- 14.下列关于基因工程的叙述正确的是( ) A所有的限制酶都能识别同一种特定的核苷酸序列 B 基因工程技术是唯一能冲破
- 默写古诗文名句。(6分) ①山重水复疑无路, 。(陆游《游山西村》)② ,载不动许多愁。
- 下列命题中的假命题是( )A.“度”与“弧度”是度量角的两种不同的度量单位B.一度的角是圆周的,一弧度的角是圆周的
- 阅读下面文章,完成1-5题。 不一样的幸福 杨晨 ①到浦东机场接朋友,从悉尼到上海,不知什么原因,飞机误了点,于是,大厅
- 电流表G的内阻为,用它测量电压时,量程为U;用它改装成量程较大的电流表时,内阻为,量程为I,这几个量的关系是( )A.
- 生物只能适应所处的环境,对外界的环境无能为力。 ( )



