七年级(初一)数学下学期下册试题
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )

A . ∠2
B . ∠3
C . ∠4
D . ∠5
无论m为何值,点A(m,5﹣2m)不可能在( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
如图,在边长为 1 的正方形网格中,三角形 ABC
中任意一点 P(x0 , y0)经平移后对应点为 P1(x0-4,y0+3),已知
A(0,2),B(4,0),C(-1,-1),将三角形 ABC
作同样的平移得到三角形 A1B1C1

-
(1) 直接写出坐标:A1(,),B1(,),C1(,);
-
(2) 三角形 A1B1C1 的面积为;
-
(3) 已知点 P 在 y 轴上,且三角形 PAC 的面积等于三角形 ABC 面积的一半,求 P 点坐标.
如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )

A . 55°
B . 35°
C . 45°
D . 30°
某校组织1000名学生参加党史知识竞赛,现随机抽取部分学生的竞赛成绩,制成如下统计图表:
频数分布表
|
分数段 |
频数 |
百分比 |
|
| | 20% |
| | 80 | |
| | 60 | 30% |
| | 20 | |
频数分布直方图

根据以上图表提供的信息,解答下列问题:
-
(1) 写出表中a、b、c的数值:
 ,
,  ,
,  .
.
-
(2) 补全频数分布直方图.
-
(3) 如果竞赛成绩95分以上(含95分)的学生获得一等奖,试估计此次党史知识竞赛该校获得一等奖的人数.
在数据25,23,21,29,28,25,22,26,28,26,26,27,25,21,29中,范围在 (包括前边的数,不包括后边的数)这一组的频数是.
(包括前边的数,不包括后边的数)这一组的频数是.
 (包括前边的数,不包括后边的数)这一组的频数是.
(包括前边的数,不包括后边的数)这一组的频数是.
已知:如图,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD.

先化简,再求值:  ,其中
,其中  ,
, 
 ,其中
,其中  ,
, 
定义新运算:a★b=a(1-b),a,b是实数。如-2★3=-2×(1-3)=4.
-
(1) 求(-2)★(-1)的值;
-
(2) 求2★
 +2★(-
+2★(-  )的值。
)的值。
下列实数中,无理数是
A .  B .
B .  C .
C . 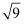 D . 0.1010010001
D . 0.1010010001
 B .
B .  C .
C . 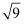 D . 0.1010010001
D . 0.1010010001
下面是两位同学在讨论一个一元一次不等式,根据对话提供的信息,他们讨论的不等式是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,直线AB、CD被直线EF所截,若AB∥CD,∠1=100°,则∠2的大小是( )

A . 10°
B . 50°
C . 80°
D . 100°
有一个数值转换器,原理如下:

当输入的x=9时,输出的y等于( )
A .  B . ±
B . ±  C .
C .  D .
D . 
 B . ±
B . ±  C .
C .  D .
D . 
在平面直角坐标系中,点P(2,-4)位于( ).
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
在实数范围内定义一种运算“*”,其规则为  ,根据这个规则求方程
,根据这个规则求方程  的解为.
的解为.
 ,根据这个规则求方程
,根据这个规则求方程  的解为.
的解为.
解不等式: 

某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:

-
(1) 这次被抽查的学生有人;请补全条形统计图;
-
(2) 在统计图2中,“乒乓球”对应扇形的圆心角是度;
-
(3) 若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有人.
已知点A的坐标为(  ),那么点A在( )
),那么点A在( )
 ),那么点A在( )
),那么点A在( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
某电器超市销售每台进价分别为200元,170元的A、B联众型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
-
(1) 求A,B两种型号的电风扇的销售单价;
-
(2) 若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
-
(3) 在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
实数  的值是( )
的值是( )
 的值是( )
的值是( )
A .  B . 8
C .
B . 8
C .  D . 4
D . 4
 B . 8
C .
B . 8
C .  D . 4
D . 4
最近更新
- 两个电子相向运动,每个电子相对于实验室的速度都是c,在实验室中观测,两个电子的总动能是多少?以一个电子为参考系,两个电子
- 某四面体的三视图如图所示,则该四面体的所有棱中最长的是 A. B. C. D.5
- The boy is ________ togreet us every morning . A.polite enou
- 下列各句中没有错别字的一句是 ( )
- 阅读下面的文字,完成问题。 人类文明与宗教 詹克明 从文明发展史来看,倘若追溯到史前时代,人类精神文明的“元胎”原本就是
- I try to understand _______ that prevents so many people fro
- Some people will do just about anything to save money. And I
- 十七大报告指出“创新是一个民族进步的灵魂,是一个国家兴旺发达的不竭动力,也是一个政党永葆生机的源泉。”树立创新意识的辩证
- 某同学列表比较了动植物细胞工程的有关内容,不正确的有 植物细胞工程 动物细胞工程 技术手段 植物组织培养 植物
- 下列描述物理量之间关系的图象中,正确的是()A. 水的质量与体积关系 B. 石子下落速度与时间的关系C. 晶体熔化温度与
- 图为一电流表的原理示意图.质量为m的均质细金属棒MN的中点处通过一挂钩与一竖直悬挂的弹簧相连,绝缘弹簧劲度系数为 k 。
- 某一导体的伏安特性曲线如AB段(曲线)所示,关于导体的电阻,以下说法正确的是() A.B点的电阻为12 Ω B.B点的电
- 关于电场强度的下列说法中,正确的是 ( ) A.电场强度与试探电荷所受电场力成正比 B.试探电荷的电荷量越
- 第四部分 写作(满分40分) 第一节 基础写作(共1小题;满分15分) 请按照下面6幅图
- 下列是关于物理学研究方法或物理学史的几种说法,其中叙述正确的是 A.探究求合力的方法实验运用了控制变量法 B.用点电荷来
- 观看下图回答:我国山脉属于南北走向的是( ) A.天山 B.昆仑山
- —Must I come tomorrow? —No, you ____. We can finish it our
- 铁及铁的化合物应用广泛,如可用作印刷电路铜板腐蚀剂。 (1)写出溶液腐蚀印刷电路铜板的离子方程式
- 读地球公转示意图,回答18~20题。18.地球公转至图中所示位置时,下列说法正确的是 A.极昼极夜的范围呈扩大趋势 B.
- 关于转录和翻译的叙述,错误的是 A.转录时以核糖核苷酸为原料B.转录时RNA聚合酶能识别DNA中特定碱基序列 C.mRN










