七年级(初一)数学下学期下册试题
若点A(a﹣2,a)在x轴上,则点B(a﹣1,3)在( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
下列事件中,为必然事件的是( )
A . 明天要下雨
B .  C .
C .  D . 打开电视机,它正在播广告
D . 打开电视机,它正在播广告
 C .
C .  D . 打开电视机,它正在播广告
D . 打开电视机,它正在播广告
解方程组: 

比较下列各数的大小,结果正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
解方程或不等式组:
-
(1)

-
(2)

如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )

A . 点B到直线l1的距离等于4
B . 点A到直线l2的距离等于5
C . 点B到直线l1的距离等于5
D . 点C到直线l1的距离等于5
0.025用科学记数法表示:.
如图,直线  相交于点
相交于点  ,已知
,已知  ,则
,则 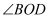 的度数为( )
的度数为( )
 相交于点
相交于点  ,已知
,已知  ,则
,则 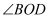 的度数为( )
的度数为( )

A .  B .
B .  C .
C . 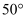 D .
D . 
 B .
B .  C .
C . 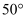 D .
D . 
解不等式组2﹣  .
.
 .
.
已知一次函数 与
与 的图象如图所示,若
的图象如图所示,若 , 则x的取值范围为( )
, 则x的取值范围为( )
 与
与 的图象如图所示,若
的图象如图所示,若 , 则x的取值范围为( )
, 则x的取值范围为( )

A . 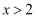 B .
B . 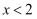 C .
C . 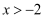 D .
D . 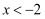
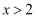 B .
B . 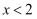 C .
C . 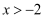 D .
D . 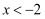
如图,在下列给出的条件中,不能判定AB∥DF的是( )

A . ∠1=∠A
B . ∠1=∠4
C . ∠A=∠3
D . ∠A+∠2=180°
如图,直线l1 , l2被l3所截得的同旁内角为a,b ,要使l1∥l2 , 只要使( ).

A . a+b =90°
B . a=b
C . 0°<a≤90°,90°≤b <180°
D . 

在下列汽车标志的图案中,能用图形的平移来分析其形成过程的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,直线a、b相交于点O,下列说法:①若∠1=∠2,则a⊥b;②若∠1=∠3,则a⊥b;③若∠1+∠3=180°,则a⊥b;④若∠1+∠2=180°,则a⊥b.其中正确的有(填序号)

小张和小陈都在电影院看电影,小张的位置用(a,b)表示,小陈的位置用(x,y)表示,我们约定“排数在前,列数在后”,若小张恰在小陈的正前方,则( )
A . a=x
B . b=y
C . a=y
D . b=x
列方程解应用题:丰收村2台大收割机和5台小收割机同时工作2h共收割小麦3.6hm2;3台大收割机和2台小收割机同时工作5h共收割小麦8hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
已知:a×  =b×1
=b×1  =c÷
=c÷  ,且a、b、c都不等于0,则a、b、c中最小的数是( )
,且a、b、c都不等于0,则a、b、c中最小的数是( )
 =b×1
=b×1  =c÷
=c÷  ,且a、b、c都不等于0,则a、b、c中最小的数是( )
,且a、b、c都不等于0,则a、b、c中最小的数是( )
A . a
B . b
C . c
D . a和c
若点 P(a-2,a+1)在 x 轴上,则 P 点的坐标为.
“十三五”以来,山西省共解决372个村、35.8万农村人口的饮水型氟超标问题,让农村群众真正喝上干净水、放心水、安全水.某公司抓住商机,根据市场需求代理  ,
,  两种型号的净水器,已知每台
两种型号的净水器,已知每台  型净水器比每台
型净水器比每台  型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进  型净水器与用4.5万元购进
型净水器与用4.5万元购进  型净水器的数量相等.
型净水器的数量相等.
 ,
,  两种型号的净水器,已知每台
两种型号的净水器,已知每台  型净水器比每台
型净水器比每台  型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进  型净水器与用4.5万元购进
型净水器与用4.5万元购进  型净水器的数量相等.
型净水器的数量相等. 
-
(1) 求每台
 型,
型,  型净水器的进价各是多少元?
型净水器的进价各是多少元?
-
(2) 该公司计划购进
 ,
,  两种型号的净水器共55台进行试销,其中
两种型号的净水器共55台进行试销,其中  型净水器为
型净水器为  台,购买两种净水器的总资金不超过10.8万元.则最多可购进
台,购买两种净水器的总资金不超过10.8万元.则最多可购进  型号净水器多少台?
型号净水器多少台?
温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
-
(1) 若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
-
(2) 若建成后的寝室可供600人住宿,求单人间的数量;
-
(3) 若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
最近更新
- (10·六盘水)下列物理量中,以科学家的名字欧姆作为单位的物理量是 A.电流 B.电阻 C.电压
- 一物体沿半径为R的圆周运动一周,其位移的大小和路程分别是( ) A.,0 B.0, C.,
- 小魔术“空瓶生烟”方法如右图:A瓶中充满氯化氢气体,B 瓶中充满氨气,抽开毛玻璃片,瓶中产生浓浓的白烟。由此回答: (1
- 蓝藻、大肠杆菌的可遗传变异来源是()A. 基因突变和染色体变异 B. 基因重组和基因突变 C. 基因突变 D. 基因重组
- ________________________,烟光凝而暮山紫。(王勃《滕王阁序》)
- ......
- 做个阳光少年,需要:①学习和生活中保持一种平淡的情绪②努力培养乐观、开朗的性格③在学习和生活中保持一种积极的心态④不断增
- It is generally considered that the key ______a foreign lang
- 如图所示电路,A、B两点间接上一电动势为4V、内电阻为1的直流电源,3个电阻的阻值均为4,电容器的电容为30F,电流表
- 认真细致的观察和分析实验现象,有助于获得化学知识并学会科学探究的方法。以下分析你认为合理的是( ) A、两种物质完全反
- 下图是某化学反应的微观示意图( )有关说法不正确的是 A、甲中的一个分子有桑原子构成 B、化学反应的实质是原子的重新组合
- 单项选择 从下列每题所给的选项中,选择一个最佳答案。 –Excuse me, sir. Smoking _______
- 在密闭容器中发生反应:aX(g)+bY(g)cZ(g)+dW(g) 反应达到平衡后,将气体体积压缩到原来的一半,当再次
- 汽车剧烈碰撞时,安全气囊中发生反应10NaN3+2KNO3= K2O+5Na2O+16N2↑。若氧化产物比还原产物多1.
- 读我国极地考察站的资料,完成问题: 极地考察站 地理坐标 建站时间 长城站 62°13′S , 62°13′W 1985
- 世界上现存最早的、标有确切日期的雕版印刷品是( ) A .《金刚经》 B.《古兰经》 C.《诗经》
- 已知:2CO(g)+O2(g)===2CO2(g) ΔH=-566 kJ/mol Na2O2(s)+CO2(g)===
- 计算:2÷=____
- 下列各组性状属于相对性状的是 A.豌豆的高茎和矮茎 B.棉纤维的长与粗 C.玉米的黄粒与圆粒 D.人的卷发与黑
- 空间探测器从某一星球表面竖直升空,已知探测器质量为500kg(设为恒量),发动机竖直推力为恒力,探测器升空后发动机因故障



