七年级(初一)数学下学期下册试题
云南省瑞丽市共诊断 例新冠肺炎确诊病例,均为缅甸输入,下列表述,能确定瑞丽位置的是( )
例新冠肺炎确诊病例,均为缅甸输入,下列表述,能确定瑞丽位置的是( )
 例新冠肺炎确诊病例,均为缅甸输入,下列表述,能确定瑞丽位置的是( )
例新冠肺炎确诊病例,均为缅甸输入,下列表述,能确定瑞丽位置的是( )
A . 云南西部
B . 云南与缅甸交界处
C . 东经 D . 东经
D . 东经 , 北纬
, 北纬
 D . 东经
D . 东经 , 北纬
, 北纬
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )

A . 25人
B . 35人
C . 40人
D . 100人
计算:  .
.
 .
.
如图,直线  被直线c所截,则下列说法中错误的是( )
被直线c所截,则下列说法中错误的是( )
 被直线c所截,则下列说法中错误的是( )
被直线c所截,则下列说法中错误的是( ) 
A . 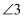 与
与  是邻补角
B .
是邻补角
B . 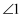 与
与 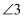 是对顶角
C .
是对顶角
C . 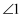 与
与 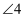 是内错角
D .
是内错角
D .  与
与 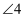 是同位角
是同位角
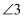 与
与  是邻补角
B .
是邻补角
B . 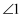 与
与 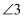 是对顶角
C .
是对顶角
C . 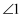 与
与 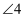 是内错角
D .
是内错角
D .  与
与 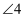 是同位角
是同位角
在平面直角坐标系中,将点  向左平移3个单位后得到点的坐标为.
向左平移3个单位后得到点的坐标为.
 向左平移3个单位后得到点的坐标为.
向左平移3个单位后得到点的坐标为.
将直线 向下平移3个单位得到的直线为.
向下平移3个单位得到的直线为.
 向下平移3个单位得到的直线为.
向下平移3个单位得到的直线为.
解下列方程组:
-
(1)
 ;
;
-
(2)
 .
.
为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对A,B两个玉米品种进行实验种植对比研究.去年A、B两个品种各种植了10亩.收获后A、B两个品种的售价均为2.4元/kg,且B品种的平均亩产量比A品种高100千克,A、B两个品种全部售出后总收入为21600元.
-
(1) 求A、B两个品种去年平均亩产量分别是多少千克?
-
(2) 今年,科技小组优化了玉米的种植方法,在保持去年种植面积不变的情况下,预计A、B两个品种平均亩产量将在去年的基础上分别增加a%和2a%.由于B品种深受市场欢迎,预计每千克售价将在去年的基础上上涨a%,而A品种的售价保持不变,A、B两个品种全部售出后总收入将增加
 a%.求a的值.
a%.求a的值.
世界科技不断发展,人们制造出的晶体管长度越来越短,某公司研发出长度只有0.000000006米的晶体管,该数用科学记数法表示为米.
如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+| b-3|=0,线段AB交y轴于F点.

-
(1) 求点A、B的坐标.
-
(2) 求点F的坐标;
-
(3) 点P为坐标轴上一点,若△ABP的面积和△ABC的面积相等,求出P点坐标.
命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A . 垂直
B . 两条直线互相平行
C . 同一条直线
D . 两条直线垂直于同一条直线
大于  而小于
而小于  的所有整数之和为.
的所有整数之和为.
 而小于
而小于  的所有整数之和为.
的所有整数之和为.
若关于  、
、  的方程组的解
的方程组的解  满足
满足 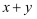 >0,则
>0,则  的取值范围是.
的取值范围是.
 、
、  的方程组的解
的方程组的解  满足
满足 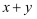 >0,则
>0,则  的取值范围是.
的取值范围是.
某企业承接了27000件产品的生产任务,计划安排甲、乙两个东间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
-
(1) 求甲、乙两个车间各有多少名工人参与生产?
-
(2) 为了提前完成生产任务,该企业设计了两种方案:
方案一:甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变;
方案二:乙车间再临时招聘若干名 工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
已知关于 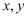 的方程组
的方程组  ,
,
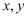 的方程组
的方程组  ,
,
-
(1) 若用代入法求解,可由①得:
 =③,把③代入②解得
=③,把③代入②解得  =,将其代入③解得
=,将其代入③解得  =,∴原方程组的解为;
=,∴原方程组的解为;
-
(2) 若此方程组的解
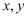 互为相反数,求这个方程组的解及
互为相反数,求这个方程组的解及  的值.
的值.
若a-b<0,则下列各式中一定正确的是( )
A . a>b
B . ab>0
C .  D . -a>-b
D . -a>-b
 D . -a>-b
D . -a>-b
实数﹣3的绝对值是( )
A . 3
B . -3
C . 0
D . 

如图,若 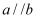 ,
, 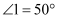 ,则
,则 
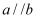 ,
, 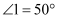 ,则
,则 

A . 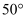 B .
B .  C .
C .  D .
D . 
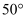 B .
B .  C .
C .  D .
D . 
将下列推理过程填写完整.

-
(1) 如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD.
证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥,(平行于同一直线的两直线平行)
-
(2) 如图2,已知∠BED=∠B+∠D,求证AB∥CD.
证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥,()
∴∥.(平行于同一直线的两直线平行)
若方程x﹣3my=2x﹣4是关于x、y的二元一次方程,则m为( )
A . m≠0
B . m≠1
C . m≠2
D . m≠3
最近更新
- 请根据括号中的中文提示、英文释义或句意,写出句中所缺单词,使句子通顺。【小题1】We students should d
- 如图所示,水平的平行虚线间距为d,其间有磁感应强度为B的匀强磁场。一个长方形线圈的边长分别为L1、L2,且L2<d,线圈
- 小杰想通过某网站购买几本书,他在收货地址中应依次写清楚自己所在的 A.省、县、村、学校
- 如图3所示,水平传送带以不变的速度v向右运动,将质量为m的工件轻轻放在传送带的左端,由于摩擦力的作用,工件做匀加速运动,
- 某种零件,标明要求是Φ:20±0.02mm(Φ表示直径).经检查,一个零件的直径是19.9 mm, 该零件
- 肾脏的结构和功能的基本单位是()A. 肾单位 B. 肾小球 C. 肾小管 D. 肾小囊
- Having drunk too much, Alfred was now driving his car
- 今年五月,长江中下游遭遇严重干旱。下列缓解旱情的做法不正确的是 A.推广使用节水器具
- 已知平面向量,且,则 A. B. C. D.
- 设,, 求:(1); (2)。
- 人体泌尿系统最重要的器官是( )A.膀胱B.肾脏C.尿道D.输尿管
- 下列不是真理标准问题讨论的结果的是() A.党中央的主要领导人仍坚持“两个凡是”的方针 B.肯定“实践是检验真理的唯一标
- 已知X和Y能发生如下反应:X+Y H2O+盐,下列有关X和Y所属种类的说法中一定不正确的是
- 右图为“我国三个经济地带划分图”,读图完成6~7题。6.关于三个经济地带发展差异的叙述,正确的是() A.东部地带社会经
- 有A 和B 两种有机物,含碳的质量分数相同,关于A 和B 的叙述正确的是A.A 和B 一定是同分异构体B.A 和B 不可
- 当太阳光线与地面成45o角时,在坡度为i=1:2 的斜坡上的一棵树AB落在坡面上的影子AC长为5米,落在水平线上的影子C
- 在生产谷氨酸过程中,常用的培养基中含有玉米浆、尿素、氯化钾、生物素等,下列说法正确的是( ) A.玉米浆属于生长因子
- 下列形容天气的语句是( ) A.夜来风雨声,花落知多少 B.四季无寒暑,一雨便成秋 C.人间四
- 已知三点A(2,3),B(-1,-1),C(6,k),其中k为常数,若||=||,则与的夹角为( ) A.arcc
- ----- Everyone in my class passed the exam. ----- Oh, real



