七年级(初一)数学下学期下册试题
若方程组  的解为
的解为 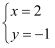 ,则a+b的值为.
,则a+b的值为.
 的解为
的解为 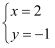 ,则a+b的值为.
,则a+b的值为.
用“△”定义一种新运算:对于任意有理数a和b,规定 , 如:
, 如:
 , 如:
, 如:
-
(1) 求
 的值;
的值;
-
(2) 若
 , 求x的值.
, 求x的值.
如图,已知∠1=∠2,∠3=∠4,∠E=90°,试问:AB∥CD吗?为什么?

解:∵∠1+∠3+∠E=180°∠E=90°
∴∠1+∠3=
∵∠1=∠2,∠3=∠4
∴∠1+∠2+∠3+∠4=
∴AB∥CD.
已知点A(﹣1,﹣3)和点B(3,m),且AB平行于x轴,则点B坐标为( )
A . (3,﹣3)
B . (3,3)
C . (3,1)
D . (3,﹣1)
已知  点在
点在  轴上,则点
轴上,则点  的坐标为.
的坐标为.
 点在
点在  轴上,则点
轴上,则点  的坐标为.
的坐标为.
计算:  .
.
 .
.
解方程
-
(1)

-
(2)
 .
.
如图,点C在射线  上,不能判定
上,不能判定  的是( )
的是( )
 上,不能判定
上,不能判定  的是( )
的是( ) 
A .  B .
B .  C .
C .  D .
D . 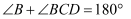
 B .
B .  C .
C .  D .
D . 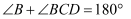
根据下列表述,能确定位置的是( )
A . 某电影院2排
B . 南京市大桥南路
C . 北偏东30°
D . 东经118°,北纬40°
为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况.小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.

回答下列问题:
-
(1) 这次被抽查的学生共有人,扇形统计图中,“B组”所对应的圆心角的度数为;
-
(2) 补全条形统计图;
-
(3) 已知该中学共有学生2500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?
根据以下程序,当输入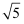 时,输出结果为( )
时,输出结果为( )
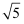 时,输出结果为( )
时,输出结果为( )
A .  B . 2
C . 6
D .
B . 2
C . 6
D . 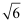
 B . 2
C . 6
D .
B . 2
C . 6
D . 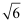
小明对某班级同学参加课外活动内容进行问卷调查后(每人必选且只选一种),绘制成如图所示的统计图,已知参加踢毽子的人数比参加打篮球的人数少6人,则参加“其他”活动的人数为人.

解不等式组  并把解在数轴上表示出来.
并把解在数轴上表示出来.
 并把解在数轴上表示出来.
并把解在数轴上表示出来.![]()
先阅读下面的文字,再回答问题:
大家知道  是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此  的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用  -1来表示、
-1来表示、  的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的.因为  的整数部分是1,所以将
的整数部分是1,所以将  减去其整数部分,所得的差就是
减去其整数部分,所得的差就是  的小数部分.
的小数部分.
例如:  <
<  <
<  ,即2<
,即2<  <3.
<3.
 的整数部分为2,小数部分为
的整数部分为2,小数部分为  -2.
-2.
-
(1) 如果
 的小数部分为a,
的小数部分为a, 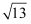 的整数部分为b,求a+b-
的整数部分为b,求a+b-  的值;
的值;
-
(2) 已知10+
 =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
如图所示, 下列条件中能判定AB∥CE的是( )

A . ∠B=∠ACB
B . ∠B=∠BAC
C . ∠B=∠ECD
D . ∠A=∠ECD
已知点  在第一象限或第三象限,则
在第一象限或第三象限,则  的取值范围是( )
的取值范围是( )
 在第一象限或第三象限,则
在第一象限或第三象限,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C . 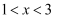 D .
D .  或
或 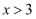
 B .
B .  C .
C . 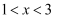 D .
D .  或
或 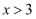
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1 , 连接AC1 , BD1 . 如果四边形ABD1C1是矩形,那么平移的距离为( )

A . 14cm
B . 16cm
C . 18cm
D . 20cm
下列实数中,不是x+4≥2的解的是( )
A . ﹣3
B . ﹣2
C . 0
D . 3.5
在平面直角坐标系中,已知点  ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点  的坐标。
的坐标。
 ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点  的坐标。
的坐标。
-
(1) 点P在x轴上;
-
(2) 点P横坐标比纵坐标大3;
-
(3) 点P在过
 点,且与y轴平行的直线上。
点,且与y轴平行的直线上。
先化简,再求值:  ,其中
,其中  .
.
 ,其中
,其中  .
.
最近更新
- Your speech given at the meeting, _____ everyoneis taking in
- 下表各组物质中,满足下图物质一步转化关系的选项是()
- 下列物质中,富含蛋白质的是A.牛奶 B.鲜橙汁 C.矿泉水 D.啤酒
- 下列物质属于纯净物的是 ( ) A. 蒸馏水 B.煤 C. 葡萄酒
- 下图中甲、乙为两个岛屿。读图回答1~2题。1.有关甲、乙两个岛屿的叙述,正确的是 () A.两岛屿都盛产柑橘、香蕉、菠
- 我国出口产品大都为资源能源、初级产品,工业制成品、深加工产品比例较小。中国还不是创造大国。据统计,国内拥有自主知识产权核
- 作文 有一位哲人说过,一个人学会了感谢,他就成熟了。在我们的成长经历中,有很多人,很多事,都给了我们帮助、教育和启迪。
- 读下表,回答17-18题。17.与江西省相比,贵州省耕地的结构特点及其原因是 A.水田比重大——属季风气候,降水丰沛 B
- 下列说法中正确的是( ) A.平均速度就是速度的平均值 B.瞬时速率是指瞬时速度的大小 C.火车以速度v经过某一段
- 草木灰的主要成分是K2CO3,其中含有少量的泥沙、KCl、K2SO4等杂质。某校的课外活动小组的同学为了测定草木灰中K2
- 下列变化属于物理变化的是A.煤的干馏 B.石油的分馏 C.重油的裂化 D.石油的裂解
- 16.用下面的短语组成两副有关春节和端午的对联。要求:上下联各为7字,语言连贯,符合节日 和对联特点,不得重复使用短语。
- 如图11,山顶有一铁塔AB的高度为20米,为测量山的高度BC,在山脚点D处测得塔顶A和塔基B的仰角分别为60º和45º,
- 世界都是一分为二的,认识世界、研究物质也是如此. (1)利用CO2、的性质可用于灭火. (2)当大气中CO2的含量升高时
- 小明站在水平地面上静止不动时,对地面的压强为10000Pa,他一只脚的面积是150cm2 ,则小明的体重是
- 假如你是李华,你的笔友Mike从电视上得知前段时间北京多个地方出现雾霾(haze),非常担心,写E-mail询问有关情况
- (10分)如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道相距l=1m,两轨道之间用R=3Ω的电阻连接,一质量m=
- 下列根据实验现象所作出的结论中一定正确的是( )A.无色试液使红色石蕊试纸变蓝,结论:该试液一定是碱溶液B.无色试
- 根据对话内容,用恰当的单词、短语或句子,补全对话 ,使对话完整通顺。(本题共5小题,每题2分,共计10分)A: Good
- 铁钉刺入某人的脚底,随即她产生了一系列的反应。此人脚底受伤后出现了红肿,医生担心她感染破伤风杆菌,立刻给她注射疫苗进行应



