弧度制、角度制及其之间的换算 知识点题库
已知扇形的圆心角的弧度数为2,扇形的弧长为4,则扇形的面积为( )
A . 2
B . 4
C . 8
D . 16
已知圆中一段弧长正好等于该圆的外切正三角形的边长,那么这段弧所对的圆心角的弧度数为 ( )
A .  B .
B .  C .
C .  D .
D . 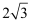
 B .
B .  C .
C .  D .
D . 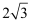
若扇形的周长为4cm,半径为1cm,则其圆心角的大小为( )
A . 2°
B . 4°
C . 2
D . 4
若一扇形的圆心角为30°,弧长为π,则其半径为( )
A . 3
B . 6
C . 3π
D . 

若一个圆锥的侧面展开图恰好是一个半圆,则这个圆锥的侧面积与表面积之比为
已知一个扇形的周长是12cm,
(1)若扇形的圆心角α=300 , 求该扇形的半径
(2)当扇形半径为何值时,这个扇形的面积最大?别求出此时的圆心角.
计算:
(1)已知扇形的周长为10,面积是4,求扇形的圆心角.
(2)已知扇形的周长为40,当他的半径和圆心角取何值时,才使扇形的面积最大?
一个扇形的弧长和面积均为5,则这个扇形圆心角的弧度数是
你的手表慢了5分钟,你是怎样将它校准的?假如你的手表快了1.25小时,你应当如何将它校准?当时间校准后,分针旋转了多少度?
将1920°转化为弧度数为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
把下列各角的弧度化为角度或把角度化为弧度:(1)﹣135° (2) .
.
 .
.
将﹣300°化为弧度为( )
A . -  B . -
B . -  C . -
C . -  D . -
D . - 
 B . -
B . -  C . -
C . -  D . -
D . - 
AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2 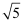 km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
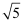 km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
km.现欲在此地块内建一形状为直角梯形DECF的科技园区. 
-
(1) 求此曲边三角形地块的面积;
-
(2) 求科技园区面积的最大值.
时钟的分针在1点到3点20分这段时间里转过的弧度数为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
英国浪漫主义诗人  (雪莱)在《西风颂》结尾写道“
(雪莱)在《西风颂》结尾写道“  ”春秋战国时期,为指导农耕,我国诞生了表示季节变迁的
”春秋战国时期,为指导农耕,我国诞生了表示季节变迁的  节气.它将黄道(地球绕太阳按逆时针方向公转的轨道,可近似地看作圆)分为
节气.它将黄道(地球绕太阳按逆时针方向公转的轨道,可近似地看作圆)分为  等份,每等份为一个节气.2019年12 月22日为冬至,经过小寒和大寒后,便是立春.则从冬至到次年立春,地球公转的弧度数约为( )
等份,每等份为一个节气.2019年12 月22日为冬至,经过小寒和大寒后,便是立春.则从冬至到次年立春,地球公转的弧度数约为( )
 (雪莱)在《西风颂》结尾写道“
(雪莱)在《西风颂》结尾写道“  ”春秋战国时期,为指导农耕,我国诞生了表示季节变迁的
”春秋战国时期,为指导农耕,我国诞生了表示季节变迁的  节气.它将黄道(地球绕太阳按逆时针方向公转的轨道,可近似地看作圆)分为
节气.它将黄道(地球绕太阳按逆时针方向公转的轨道,可近似地看作圆)分为  等份,每等份为一个节气.2019年12 月22日为冬至,经过小寒和大寒后,便是立春.则从冬至到次年立春,地球公转的弧度数约为( )
等份,每等份为一个节气.2019年12 月22日为冬至,经过小寒和大寒后,便是立春.则从冬至到次年立春,地球公转的弧度数约为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 化为弧度,结果是.
化为弧度,结果是.
给出下列3个结论,其中正确的个数是( )
①  是第三象限角;②
是第三象限角;②  是第二象限角;③
是第二象限角;③  .
.
A . 3
B . 2
C . 1
D . 0
把下列各角的弧度数化为度数,度数化为弧度数.
-
(1)
 ;
;
-
(2)
 ;
;
-
(3) 1125° ;
-
(4) -225°.
下列结论中正确的是( )
A . 终边经过点  的角的集合是
的角的集合是  B . 将表的分针拨慢10分钟,则分针转过的角的弧度数是
B . 将表的分针拨慢10分钟,则分针转过的角的弧度数是  C . 若
C . 若  是第三象限角,则
是第三象限角,则  是第二象限角,
是第二象限角,  为第一或第二象限角
D .
为第一或第二象限角
D .  ,
,  ,则M⫋N
,则M⫋N
 的角的集合是
的角的集合是  B . 将表的分针拨慢10分钟,则分针转过的角的弧度数是
B . 将表的分针拨慢10分钟,则分针转过的角的弧度数是  C . 若
C . 若  是第三象限角,则
是第三象限角,则  是第二象限角,
是第二象限角,  为第一或第二象限角
D .
为第一或第二象限角
D .  ,
,  ,则M⫋N
,则M⫋N
下列选项正确的是( )
A .  B .
B .  C . 若
C . 若  终边上有一点
终边上有一点  ,则
,则  D . 若一扇形弧长为2,圆心角为
D . 若一扇形弧长为2,圆心角为  ,则该扇形的面积为
,则该扇形的面积为 
 B .
B .  C . 若
C . 若  终边上有一点
终边上有一点  ,则
,则  D . 若一扇形弧长为2,圆心角为
D . 若一扇形弧长为2,圆心角为  ,则该扇形的面积为
,则该扇形的面积为 
最近更新
- 甲、乙两名射手在一次射击中的得分为两个相
- 已知复数,,那么的最大值是 �
- 18.补写出下列名句名篇中的空缺部分。(6分
- —What language are they speaking? —I’m not sure
- 用NA表示阿伏加德罗常数的值。下列叙述正确
- 已知函数f(x)=log4(4x+1)+kx(k∈R)为偶函数. (1)
- 常温下pH=6的盐酸和pH=6的NH4Cl溶液,其中由
- “两会”的共同之处在于( ) ①都坚持中国
- 3.著名历史学家黄仁宇在他的《中国大历史
- 若样本1+x1,1+x2,1+x3,…,1+xn的平均数是1
- (11分)Cu—Fe合金由于长时间置于空气中表面
- “两全等三角形的面积相等”改写成“若p则q
- 已知关于x的一元二次方程x2-(m-1)x+m+2
- 用烧碱进行处理时,发生如下两个反应:NaOH+H
- 2010年甲企业生产M商品的价值量和价值总量
- 补写出下列名篇名句中的空缺部分。 (1)_______
- 下列活动中,不属于农业生产活动的是 �
- 图①是一面矩形彩旗完全展平时的尺寸图(单
- 【2016·湖南省张家界卷】 (一)阅读下面的
- 政党区别于其他一切政治组织的根本标志是 (



