七年级(初一)数学下学期下册试题
已知 , 则代数式
, 则代数式 的值是( )
的值是( )
 , 则代数式
, 则代数式 的值是( )
的值是( )
A . -5
B . 5
C . 13
D . 1
在实数范围内定义新运算:  ;若不等式
;若不等式  的解集是
的解集是 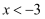 ,则
,则  的值是.
的值是.
 ;若不等式
;若不等式  的解集是
的解集是 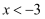 ,则
,则  的值是.
的值是.
把命题“对顶角相等”改写成“如果……,那么……”的形式:.
-
(1) 采用夹逼法,利用
 的一系列不足近似值和过剩近似值来估计它的大小的过程如下:
的一系列不足近似值和过剩近似值来估计它的大小的过程如下:
∵
 ,
,∴

∵
 ,
,  ,
,∴

∵
 ,
,∴

∵
 ,
,∴

因此
 (精确到百分位),
(精确到百分位),使用夹逼法,求出
 的近似值(精确到百分位).
的近似值(精确到百分位). -
(2) 我们规定用符号
 表示数
表示数  的整数部分,例如
的整数部分,例如 
①按此规定
 ;
;②如果
 的整数部分是
的整数部分是  的小数部分是
的小数部分是  求
求  的值.
的值.
下列说法正确的是( )
A . 每个定理都有逆定理
B . 真命题的逆命题都是真命题
C . 每个命题都有逆命题
D . 假命题的逆命题都是假命题
已知  是方程
是方程  的解,那么k的值为( )
的解,那么k的值为( )
 是方程
是方程  的解,那么k的值为( )
的解,那么k的值为( )
A . -1
B . 1
C .  D .
D . 
 D .
D . 
完成下面的计算,并在括号内标注理由.
如图,直线a、b被直线c、d所截,∠1=75°,∠2=75°,∠3=60°.求∠4的度数.

解:∵∠1=75°,∠2=75°, ∴∠1=∠2.
∴∥().
∴+=( ).
∵∠3=60°,∴∠4=°.
为了了解本地区老年人一年中生病的次数,下列收集数据的方式最合理的是( )
A . 到公园里调查100名晨练老人
B . 到医院调查100名老年病人
C . 调查10名老年邻居;
D . 利用派出所户籍资料,按抽样规则抽查本地区10%的老年人
已知代数式 的值不小于代数式
的值不小于代数式 的值,试确定
的值,试确定 的最小整数值.
的最小整数值.
 的值不小于代数式
的值不小于代数式 的值,试确定
的值,试确定 的最小整数值.
的最小整数值.
如图是甲、乙两户居民家庭全年支出费用的扇形统计图.根据统计图,下面对全年食品支出费用判断正确的是( )
A . 甲户比乙户多
B . 乙户比甲户多
C . 甲、乙两户一样多
D . 无法确定哪一户多
已知方程组 , 以下说法正确的是( )
, 以下说法正确的是( )
 , 以下说法正确的是( )
, 以下说法正确的是( )
A . 无论实数 取何值,
取何值, 不可能等于
不可能等于 B . 当
B . 当 时,方程组的解也是方程
时,方程组的解也是方程 的解
C . 存在某一个
的解
C . 存在某一个 值,使得
值,使得 ,
,  D . 代数式
D . 代数式 的最小值为7
的最小值为7
 取何值,
取何值, 不可能等于
不可能等于 B . 当
B . 当 时,方程组的解也是方程
时,方程组的解也是方程 的解
C . 存在某一个
的解
C . 存在某一个 值,使得
值,使得 ,
,  D . 代数式
D . 代数式 的最小值为7
的最小值为7
已知x +4y-3z = 0,且4x-5y + 2z = 0,x:y:z 为( )
A . 1:2:3
B . 1:3:2
C . 2:1:3
D . 3:1:2
已知关于x,y的二元一次方程组 

-
(1) 若方程组的解 x,y的值互为相反数,求k的值;
-
(2) 若方程组的解x,y的值满足x<1,且
 ,求k的取值范围.
,求k的取值范围.
如果x∶y=5∶2,并且满足x-3y=-7,则x、y中较小的是( )
A . 35
B . -14
C . -35
D . 14
已知点P(2-m,m-5)在第三象限,则整数m的值是( )
A . 4
B . 3,4
C . 4,5
D . 2,3,4
为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是( )
A . 某市八年级学生的肺活量
B . 从中抽取的500名学生的肺活量
C . 从中抽取的500名学生
D . 500
化简:(25+4  )0﹣(﹣1)2012+|﹣
)0﹣(﹣1)2012+|﹣  |=.
|=.
 )0﹣(﹣1)2012+|﹣
)0﹣(﹣1)2012+|﹣  |=.
|=.
若a>0,则点P(-a,2)位于( )
A . 第四象限
B . 第三象限
C . 第二象限
D . 第一象限
下列语句中,真命题有( )个
①在同一平面内,过一点有且只有一条直线与已知直线平行;
②相等的角是对顶角;
③若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角;
④平方根和立方根相等的数是0;
⑤平移变换中,各组对应点连成的线段平行且相等.
A . 1
B . 2
C . 3
D . 4
若不等式组  无解,则不等式组
无解,则不等式组  的解集是( )
的解集是( )
 无解,则不等式组
无解,则不等式组  的解集是( )
的解集是( )
A .  B .
B .  C .
C .  D . 无解
D . 无解
 B .
B .  C .
C .  D . 无解
D . 无解
最近更新
- 下列加点的词语古今意义不相同的一项是…( ) A.开国何茫然 B.然后天梯石栈相
- (2007·全国Ⅱ,31)有一个珠宝商一生致力于珠宝的真伪之辨,技艺炉火纯青。一天,他看到一个孩子将真假珠宝混在一起当作
- A、B、C为3种单质(其中A为固体,B、C为气体),将D的饱和溶液滴入沸水中继续煮沸,溶液呈红褐色,B、C反应的产物易
- To save class time,our teacher has_______students do half of
- 早在春秋战国时期,我国就开始生产和使用铁器.下列说法正确的是()A.铁和铁合金都容易被腐蚀 B.高炉炼铁是利用还原剂在高
- 在生命活动中,酶是不可缺少的生物催化剂,以下四种酶的作用部位分别是 ①转氨酶 ②解旋酶
- 在下列机械中,A羊角锤,B钓鱼竿,C天平,D筷子,E铁匠剪刀,其中属于省力杠杆的是__________;属于费力杠杆的是
- 黄粉虫幼虫生活在较暗的环境中。在探究“光对黄粉虫幼虫生活的影响”的实验中,把同样多的黄粉虫幼虫问日寸放在较暗和较亮的环境
- We can talk with friends on the Internet _______ it’s easier
- 某校同学开展了如图所示“溶液酸碱性的检验”的实验活动: (1)把自制的紫薯汁按图1所示分别滴加到试管中,观察到的现象如下
- 在中,若, 则这个三角形是( )A. 直角三角形 B. 锐角三角形
- 用螺旋测微器(千分尺)测量金属丝的直径时,示数如下图所示.这时读出的数值是__________mm.
- (本题8分)长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了
- 如图为一个立方体的表面展开图,现将它折叠成立方体,则与数字1相对的面上标有的数字是 ▲ .
- 光合作用与化能合成作用的相似点是 A.都以太阳能作为能源 B.都需要环境中的物质氧化释放能量
- 下列对甲~丁图所示的生命活动或生物现象变化曲线的叙述,正确的是( )A.甲图中,曲线BC段的生理效应是随着生长素浓
- 辽宁沈阳二中2010届上学期高三第四次阶段测试 --- Why didn’t you come to his party
- 二茂铁[(C5H5)2Fe]是由一个二价铁离子和2个环戊烯基负离子构成,它的发现可以说是有机金属化合物研究中具有里程碑意
- 2014年2月12日新疆于田县发生7.3级地震,政府相关部门立即安排了救援行动。据此回答8~9题。 8.在第一时间掌握整
- 第二次工业革命极大地促进了世界经济的互动的整体化趋势,世界市场进一步发展。为论证该观点,你将选择的证据是( ) ①



