七年级(初一)数学下学期下册试题

-
(1) 在AC边求作点E,使得DE∥AB;(要求:尺规作图,不写作法,保留作图痕迹)
-
(2) 在(1)的条件下,若∠ABC=40°,∠ACB=2∠CDE,求∠ACB的度数.
例如:计算  .
.
此题我们按照常规的运算方法计算比较复杂,但如果采用下面的方法把乘法转化为减法后计算就变得非常简单.
分析方法:因为  ,
,  ,
,  ,
,  .
.
所以,将以上4个等式两边分别相加即可得到结果,解法如下:




-
(1)
 ;
;
-
(2) 应用上面的方法计算:
 .
.
-
(3) 类比应用上面的方法探究并计算:
 .
.
 是3的一个平方根
D . 25的算术平方根是±5
是3的一个平方根
D . 25的算术平方根是±5
 ,
,  ,
,  ,
,  ,…,利用以上的运算规律写出
,…,利用以上的运算规律写出  = ,计算:
= ,计算:  =.
=.
-
(1)

-
(2)
 .
.

-
(1) 建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得
 ,即
,即 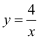 ;由周长为m,得
;由周长为m,得  ,即
,即  .满足要求的
.满足要求的  应是两个函数图象在第象限内交点的坐标.
应是两个函数图象在第象限内交点的坐标. -
(2) 画出函数图象
函数
 的图象如图所示,而函数
的图象如图所示,而函数  的图象可由直线
的图象可由直线  平移得到.请在同一直角坐标系中直接画出直线
平移得到.请在同一直角坐标系中直接画出直线  .
. -
(3) 平移直线
 ,观察函数图象
,观察函数图象 ①当直线平移到与函数
 的图象有唯一交点
的图象有唯一交点  时,周长m的值为 ▲ ;
时,周长m的值为 ▲ ;②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
-
(4) 得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为.
-
(1) 第一批牛奶进货单价为多少元?
-
(2) 超市销售两批牛奶售价相同,两批全部售完后要求获利不少于4000元,则售价至少为多少元?

-
(1) 补全频数直方图;
-
(2) 若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
-
(3) 比赛共设一、二、三等奖,若只有15%的参赛同学能拿到一等奖,则一等奖的最低分数线是多少?

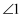 和
和  是对顶角的是( )
是对顶角的是( )
 ,点A在直线l1上,以点A为圆心,适当长度为半径画弧,分别交直线l1 , l2于B,C两点,连接AC,BC.若∠ABC=65°,则∠1的大小为( )
,点A在直线l1上,以点A为圆心,适当长度为半径画弧,分别交直线l1 , l2于B,C两点,连接AC,BC.若∠ABC=65°,则∠1的大小为( ) 
 ;②无理数是无限小数;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是( )
;②无理数是无限小数;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是( )
黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:

-
(1) 本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
-
(2) 本次抽样调查中,学习时间的中位数落在哪个等级内?
-
(3) 表示B等级的扇形圆心角α的度数是多少?
-
(4) 在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.

-
(1) 现有长方形铁片2014张,正方形铁片1176张,如果将两种铁片刚好全部用完,则可加工的竖式和横式长方体铁容器各有多少个?
-
(2) 把长方体铁容器加盖可以加工成铁盒.现工厂准备将35块铁板裁剪成长方形铁片和正方形铁片,用来加工铁盒,已知1块铁板可裁成3张长方形铁片或4张正方形铁片,也可以裁成1张长方形铁片和2张正方形铁片.问:该工厂充分利用这35张铁板,最多可以加工成多少铁盒?
 ﹣3最接近的整数是.
﹣3最接近的整数是.
 ,
,

①画出△ABC和△A1B1C1的对称中心  ;
;
②将△A1B1C1沿直线 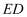 方向向上平移6格,得到△A2B2C2 , 画出△A2B2C2;
方向向上平移6格,得到△A2B2C2 , 画出△A2B2C2;
③将△A2B2C2绕点C2顺时针方向旋转90°,得到△A3B3C3 , 画出△A3B3C3.
①连接BB1、CC1 , 线段BB1与线段CC1的交点为O,点O就是所求的对称中心.
②如图△A2B2C2就是所求的三角形.
③如图△A3B3C3就是所求的三角形.

 ,点
,点  是
是  之间的任意一点且在
之间的任意一点且在  右侧.
右侧. 
-
(1)
 与
与  的数量关系是;
的数量关系是;
-
(2)
 的平分线所在直线与
的平分线所在直线与  的邻补角平分线相交于点
的邻补角平分线相交于点  .
. ①根据题意,在图中补全图形,判断
 与
与  的数量关系并说明理由;
的数量关系并说明理由;②若
 ,求
,求  的度数(用含
的度数(用含  的式子表示).
的式子表示).

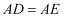 , 则数轴上点E所表示的数为.
, 则数轴上点E所表示的数为. 
- 综合探究 在日复一日的时间河流里,节日就像一个个停泊的码头,人们徜徉其间,体味某种特定的情景,把情绪调到兴奋的波段,尽情
- 下图为人体的泌尿系统示意图。下列有关叙述中,正确的是()A.尿素是在甲处形成的 B.乙是人体内唯一有排泄功能的器官 C.
- 下列物质属于有机物的是: A.氰化钾(KCN) B.碳酸氢钾(KHCO3) C.乙炔(C2H2)
- 这是某中学学生的爱好调查表。请仔细阅读,先描述该调查的结果,然后选择其中两项内容发表你自己的观点,并说明赞成或不赞成的原
- 如图所示,半径为R的圆桶内有一质量为m的物体贴着内壁跟随桶以角速度ω作匀速圆周运动,此时桶壁受到的压力的大小为
- 化学实验要操作规范,更要保障安全。下列实验操作符合这一要求的是 A. 滴管伸入试管可以准确地把液体滴入试管 B.实验中未
- 受精是指( ) A.产生卵细胞的过程 B.产生精子的过程 C.精子和卵细胞结合的过程
- 生物体内既能储存能量,又能为生命活动直接提供能量的物质是() A. 葡萄糖 B. 糖原 C. 三磷酸腺苷 D. 脂肪
- 小君和小英同学发现:带火星的竹签在空气中不会复燃,若用装有60%水的集气瓶倒置在水槽中收集氧气,得到的气体能使带火星的竹
- 1.下列各句中,没有语病的一句是( ) A. 《中国诗词大会》紧紧抓住了中国受众的诗词文化情结,对于中国古典诗词的
- 若集合= ( ) A. B. C.[—1,0] D.
- 右下图为细胞膜的亚显微结构模式图,下列关于细胞膜结构和功能的说法错误的是A. 组成细胞膜的化学元素是C、H、O、N B.
- 调查法是生态学常用的研究方法,下列有关叙述正确的是( ) A.调查土壤中小动物类群丰富度常用取样器取样法 B.样方法
- 函数,.当时,x的范围是A.x<-1B.-1<x<2C.x<-1或x>2D.x>2
- ......
- 虚拟现实技术是一种可以创建和体验虚拟世界的计算机仿真系统,它通过交互式的三维动态视景和实体行为的系统仿真,使用户沉浸到计
- 人类的生产和生活都离不开水。 (1)右图所示的实验,试管a中得到的气体为______________; 有关反应的化学方
- 阅读下面文章,完成1—4题。 爱,从来不卑微 ①很长一段时间,我一直为生命的某些命题所困扰。关于人生价值,关于人间真情等
- 下列文字表述与反应方程式对应且正确的是( ) A.溴乙烷中滴入AgNO3溶液检验其中的溴元素:Br-+Ag+==A
- “盐泥”是粗盐提纯及电解食盐水过程中形成的工业“废料”。某工厂的盐泥 含有NaCl(15~20%)、Mg(OH)2(1



