简谐运动 知识点题库
一竖直悬挂的弹簧振子,下端装有一记录笔,在竖直面内放置有一记录纸。当振子上下振动时,以速率v水平向左匀速拉动记录纸,记录笔在纸上留下如图所示的图像,y1、y2、x0、2x0为纸上印迹的位置坐标。由此图求振动的周期和振幅。

做简谐运动的弹簧振子质量为0.2 kg,当它运动到平衡位置左侧20 cm时,受到的回复力是4 N;当它运动到平衡位置右侧40 cm时,它的加速度为m/s2 , 方向为。
如图,a、b、c、d是均匀媒质中x轴上的四个质点.相邻两点的间距依次为2m、4m和6m.一列简谐横波以2m/s的波速沿x轴正向传播,在t=0时刻到达质点a处,质点a由平衡位置开始竖直向下运动,t=3s时质点a第一次到达最高点.下列说法正确的是( )
![]()
A . 在t=6s时刻波恰好传到质点d处
B . 在t=5s时刻质点c恰好到达最高点
C . 质点b开始振动后,其振动周期为4s
D . 在4s<t<6s的时间间隔内质点c向上运动
关于简谐运动的位移、加速度和速度的关系,下列说法中正确的是( )
A . 位移减少时,加速度减少,速度也减少
B . 位移方向总是跟加速度方向相反,跟速度方向相同
C . 物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背离平衡位置时,速度方向跟位移方向相同
D . 物体向负方向运动时,加速度方向跟速度方向相同;向正方向运动时,加速度方向跟速度方向相反
如图所示,弹簧振子在BC间振动,O为平衡位置,BO=OC=5cm,若振子从B到C的运动时间是1s,则下列说法中正确的是( )
![]()
A . 振子从B经O到C完成一次全振动
B . 振动周期是1 s,振幅是10 cm
C . 经过两次全振动,振子通过的路程是20 cm
D . 从B开始经过3 s,振子通过的路程是30 cm
如图所示,质量为M=0.5kg的框架B放在水平地面上.劲度系数为k=100N/m的轻弹簧竖直放在框架B中,轻弹簧的上端和质量为m=0.2kg的物体C连在一起.轻弹簧的下端连在框架B的底部.物体C在轻弹簧的上方静止不动.现将物体C竖直向下缓慢压下一段距离x=0.03m后释放,物体C就在框架B中上下做简谐运动.在运动过程中,框架B始终不离开地面,物体C始终不碰撞框架B的顶部.已知重力加速度大小为g=10m/s2 . 试求:当物体C运动到最低点时,物体C的加速度大小和此时物体B对地面的压力大小.

以下说法中不正确的是( )
A . 简谐运动中回复力总指向平衡位置
B . 太阳光是偏振光
C . 电磁波是横波,它的传播不需要介质
D . 家电的遥控器是利用红外线的遥感
简谐运动是我们研究过的一种典型运动方式.

-
(1) 一个质点做机械振动,如果它的回复力与偏离平衡位置的位移大小成正比,而且方向与位移方向相反,就能判定它是简谐运动.如图1所示,将两个劲度系数分别为k1和k2的轻质弹簧套在光滑的水平杆上,弹簧的两端固定,中间接一质量为m的小球,此时两弹簧均处于原长.现将小球沿杆拉开一段距离后松开,小球以O为平衡位置往复运动.请你据此证明,小球所做的运动是简谐运动.
-
(2) 以上我们是以回复力与偏离平衡位置的位移关系来判断一个运动是否为简谐运动.但其实简谐运动也具有一些其他特征,如简谐运动质点的运动速度v与其偏离平衡位置的位移x之间的关系就都可以表示为v2=v02﹣ax2 , 其中v0为振动质点通过平衡位置时的瞬时速度,a为由系统本身和初始条件所决定的不变的常数.请你证明,图2中小球的运动也满足上述关系,并说明其关系式中的a与哪些物理量有关.已知弹簧的弹性势能可以表达为
 ,其中k是弹簧的劲度系数,x是弹簧的形变量.
,其中k是弹簧的劲度系数,x是弹簧的形变量.
-
(3) 一质点沿顺时针方向以速度v0做半径为R的匀速圆周运动,如图所示.请结合第(2)问中的信息,分析论证小球在x方向上的分运动是否符合简谐运动这一特征.
下列说法中正确的是( ) )
A . 做简谐运动的质点,离开平衡位置的位移相同时,加速度也相同
B . 做简谐运动的质点,经过四分之一个周期,所通过的路程一定是一倍振幅
C . 变化的磁场可以产生稳定的电场,变化的电场可以产生稳定的磁场
D . 双缝干涉实验中,若只减小双缝到光屏间的距离,两相邻亮条纹间距将变大
E . 声波从空气传入水中时频率不变,波长变长
-
(1) 一简谐横波沿x轴正方向传播,在t=
 时刻,该波的波形图如图(a)所示,P、Q是介质中的两个质点。图(b)表示介质中某质点的振动图像。下列说法正确的是
时刻,该波的波形图如图(a)所示,P、Q是介质中的两个质点。图(b)表示介质中某质点的振动图像。下列说法正确的是  A . 质点Q的振动图像与图(b)相同 B . 在t=0时刻,质点P的速率比质点Q的大 C . 在t=0时刻,质点P的加速度的大小比质点Q的大 D . 平衡位置在坐标原点的质点的振动图像如图(b)所示 E . 在t=0时刻,质点P与其平衡位置的距离比质点Q的大
A . 质点Q的振动图像与图(b)相同 B . 在t=0时刻,质点P的速率比质点Q的大 C . 在t=0时刻,质点P的加速度的大小比质点Q的大 D . 平衡位置在坐标原点的质点的振动图像如图(b)所示 E . 在t=0时刻,质点P与其平衡位置的距离比质点Q的大 -
(2) 如图,一般帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m。距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8)。已知水的折射率为

(i)求桅杆到P点的水平距离;
(ii)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍然照射在桅杆顶端,求船行驶的距离。

如图所示,波源S形成的简谐横波在均匀介质中向左、右传播,P、Q两质点位于波源S的两侧,且P、Q和S的平衡位置在一条直线上,P、Q的平衡位置到S的平衡位置之间的距离分别为14.6m、13.4m。已知波源振动的频率为20Hz,波速为16m/s,当P、Q开始振动后,下列判断正确的是( )
![]()
A . P、Q两质点运动的方向始终相同
B . P、Q两质点运动的方向始终相反
C . 当S恰好通过平衡位置向上运动时,Q在波峰
D . 当S恰好通过平衡位置时,P、Q两点也正好通过平衡位置
关于机械波,下列说法正确的是( )
A . 质点振动的方向总是垂直于波传播的方向
B . 机械波可以在真空中传播
C . 任一振动质点每经过一个周期沿波的传播方向移动一个波长
D . 振动相位总是相同的两个相邻质点间的距离为一个波长
弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.2s时,振子速度第一次变为-v;在t=0.5s时,振子速度第二次变为-v.
-
(1) 求弹簧振子振动周期T.
-
(2) 若B、C之间的距离为25cm,求振子在4.0s内通过的路程.
-
(3) 若B、C之间的距离为25cm.从平衡位置计时,写出弹簧振子位移表达式,并画出弹簧振子的振动图象.
我们已经学过了关于两个质点之间万有引力的大小是:F=  .但是,在某些特殊情况下,非质点之间的万有引力计算及其应用的问题,我们可以利用下面两个已经被严格证明是正确的结论,而获得快速有效地解决:
.但是,在某些特殊情况下,非质点之间的万有引力计算及其应用的问题,我们可以利用下面两个已经被严格证明是正确的结论,而获得快速有效地解决:
 .但是,在某些特殊情况下,非质点之间的万有引力计算及其应用的问题,我们可以利用下面两个已经被严格证明是正确的结论,而获得快速有效地解决:
.但是,在某些特殊情况下,非质点之间的万有引力计算及其应用的问题,我们可以利用下面两个已经被严格证明是正确的结论,而获得快速有效地解决: a.若质点m放置在质量分布均匀的大球壳M(球壳的厚度也均匀)的空腔之内,那么m和M之间的万有引力总是为零.
b.若质点m放置在质量分布均匀的大球体M之外(r≥r0),那么它们之间的万有引力为:F=  ,式中的r为质点m到球心之间的距离; r0为大球体的半径.
,式中的r为质点m到球心之间的距离; r0为大球体的半径.
假设地球可视为一个质量分布均匀且密度为ρ的球体,通过地球的南北两极之间能够打通一个如图所示的真空小洞.若地球的半径为R,万有引力常数为G,把一个质量为m的小球从北极的洞口由静止状态释放后,小球能够在洞内运动.

-
(1) 求:小球运动到距地心为0.5R处的加速度大小a;
-
(2) 证明:小球在洞内做简谐运动;
-
(3) 求:小球在运动过程中的最大速度vm .
如图所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量大于乙的质量.当细线突然断开后,两物块都开始做简谐运动,在运动过程中( ).

A . 甲的振幅大于乙的振幅
B . 甲的振幅小于乙的振幅
C . 甲的最大速度小于乙的最大速度
D . 甲的最大速度大于乙的最大速度
-
(1) 如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2s内经过的路程为0.4m。该弹簧振子的周期为s,振幅为m。

-
(2) 将两块半径均为R、完全相同的透明半圆柱体A、B正对放置,圆心上错开一定距离,如图所示,用一束单色光沿半径照射半圆柱体A,设圆心处入射角为
 ,当
,当  时,A右侧恰好无光线射出;当
时,A右侧恰好无光线射出;当  时,有光线沿B的半径射出,射出位置与A的圆心相比下移h,不考虑多次反射,求:
时,有光线沿B的半径射出,射出位置与A的圆心相比下移h,不考虑多次反射,求: 
(i)半圆柱体对该单色光的折射率;(ii)两个半圆柱体之间的距离d。
如图所示,弹簧振子在B、C两点间做无摩擦的往复运动,O是振子的平衡位置。则振子( )

A . 从B向O运动过程中位移一直变小
B . 从O向C运动过程中加速度一直变小
C . 从B经过O向C运动过程中速度一直变大
D . 从C经过O向B运动过程中弹性势能一直变大
一个水平弹簧振子的振动图像如图所示,已知小球质量为  ,弹簧的劲度系数为
,弹簧的劲度系数为  ,下列说法正确的是( )
,下列说法正确的是( )
 ,弹簧的劲度系数为
,弹簧的劲度系数为  ,下列说法正确的是( )
,下列说法正确的是( ) 
A . 小球位移随时间变化的关系式为  B . 在第
B . 在第  末到第
末到第 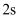 末这段时间内,小球的动能在减少、弹性势能在增加
C . 小球的最大加速度为
末这段时间内,小球的动能在减少、弹性势能在增加
C . 小球的最大加速度为  D . 该小球在
D . 该小球在  内的位移为
内的位移为  ,路程为
,路程为 
 B . 在第
B . 在第  末到第
末到第 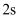 末这段时间内,小球的动能在减少、弹性势能在增加
C . 小球的最大加速度为
末这段时间内,小球的动能在减少、弹性势能在增加
C . 小球的最大加速度为  D . 该小球在
D . 该小球在  内的位移为
内的位移为  ,路程为
,路程为 
弹簧振子在做机械振动时,按周期性规律变化的物理量是( )
A . 回复力
B . 周期
C . 频率
D . 振幅
一列向右传播的简谐横波传到 R 点时的波形如图所示,波速为v=0.06 m/s,质点 P、Q 的坐标分别为 XP=0.96 m,XQ=0.36 m。求:

-
(1) 质点 P 开始振动时的振动方向;
-
(2) 从图示时刻经多长时间,质点 P 第一次到达波谷;
-
(3) 质点 P 到达波峰时,质点 Q 在何处。
最近更新
- 证明:(1)logb=logb;(2)logab=.
- the bad traffic, I was late for school thismorning.
- 相关反应式的书写:(1)光合作用的反应式(课本上)______________ ___
- 决定DNA遗传特异性的是( ) A.脱氧核糖核苷酸链上磷酸和脱氧核糖的排列顺序 B.嘌呤总数与嘧啶总数的比值 C.
- 已知椭圆,右焦点为,求连接和椭圆上任意一点的线段的中点的轨迹方程.
- 下列说法正确的是 A.空气中氧气的质量分数为21% B. 空气中各成分所占的比例是永恒不变的 C.空气是由多种物质组成的
- 矿泉水目前已成为人们常用的饮料,市场上有些不法商贩为牟取暴利,用自来水冒充矿泉水出售,为辨别真假,可用下列的一种化学试剂
- 下列有关溶液的说法,不正确的是 A.蔗糖溶液是均一的、稳定的混合物 B.硝酸钾在20℃时溶解度是31.6g,则lOOg
- 关于下图所示生物或细胞的叙述,正确的是 A. abcd均在DNA中储存
- ---So can I ask you a few personal questions?---No problem.
- It’s time to say goodbye to my school. I’ll always remember
- 2009年公务员考试中,竞争南京地区500多个职位的考生近2万人,某些职位报考出现“百里竞一”现象。这启示我们,要树立
- 通过文学来了解中国封建社会由盛转衰的历史,可读性最强的作品是 ( )A.“三言“二拍” B.《红楼梦》
- 设集合I={-2,-1,0,1,2},A={1,2},B={-2,-1,2},则A∪(B)等于( )A.{1}
- 下列各句中,没有语病的一句是 A.在中国历史上的科举时代,八十老童生和二十少状元是很正常的;有些人终老科插,有些人少年时
- 我国政府肩负着宏观调控的重任,为保障国民经济平稳运行经常会打出“组合拳”。下列政策、措施最有可能成为“组合拳”的是 A.
- 当某金属阳离子变成相应的金属时,叙述正确的是() A.得到电子被氧化 B.失去电子被还原 C.得到电子被还原
- My 14yearold son,John,and I spotted the coat which was han
- 在下列句子横线上依次填入词语,最恰当的一组是( ) (1)苏校长待人,但在执行制度方面却特别严格,不讲情面。 (2
- 下列各选项中的杂质,欲用括号内物质除去,其中能达到目的的是 A.CO2中有少量CO(灼热的氧化铜) B.CaO中



