дәҢз»ҙеҪўејҸзҡ„жҹҜиҘҝдёҚзӯүејҸ зҹҘиҜҶзӮ№йўҳеә“
иӢҘx2+y2=8 пјҢеҲҷ2xпјӢyзҡ„жңҖеӨ§еҖјдёә( )
A . 8
B . 4
C .  D . 5
D . 5
 D . 5
D . 5
и®ҫa пјҢ b пјҢ CдёәжӯЈж•°пјҢ
жұӮиҜҒпјҡ  .
.
е·ІзҹҘ m>1 дё”е…ідәҺ x зҡ„дёҚзӯүејҸ зҡ„и§ЈйӣҶдёә [0,4] .
зҡ„и§ЈйӣҶдёә [0,4] .
 зҡ„и§ЈйӣҶдёә [0,4] .
зҡ„и§ЈйӣҶдёә [0,4] .в‘ жұӮ m зҡ„еҖјпјӣ
в‘ЎиӢҘ a пјҢ b еқҮдёәжӯЈе®һж•°пјҢдё”ж»Ўи¶і a+b=m пјҢжұӮ a2+b2 зҡ„жңҖе°ҸеҖј.
е·ІзҹҘa +b
+b =1пјҢеҲҷд»ҘдёӢжҲҗз«Ӣзҡ„жҳҜпјҲгҖҖгҖҖпјү
=1пјҢеҲҷд»ҘдёӢжҲҗз«Ӣзҡ„жҳҜпјҲгҖҖгҖҖпјү
 +b
+b =1пјҢеҲҷд»ҘдёӢжҲҗз«Ӣзҡ„жҳҜпјҲгҖҖгҖҖпјү
=1пјҢеҲҷд»ҘдёӢжҲҗз«Ӣзҡ„жҳҜпјҲгҖҖгҖҖпјү
A . a2+b2пјһ1
B . a2+b2=1
C . a2+b2пјң1
D . a2b2=1
з”ЁжҹҜиҘҝдёҚзӯүејҸжұӮеҮҪж•°y= зҡ„жңҖеӨ§еҖјдёәпјҲгҖҖгҖҖпјү
зҡ„жңҖеӨ§еҖјдёәпјҲгҖҖгҖҖпјү
 зҡ„жңҖеӨ§еҖјдёәпјҲгҖҖгҖҖпјү
зҡ„жңҖеӨ§еҖјдёәпјҲгҖҖгҖҖпјү
A .  B . 3
C . 4
D . 5
B . 3
C . 4
D . 5
 B . 3
C . 4
D . 5
B . 3
C . 4
D . 5
е·ІзҹҘx2+4y2+kz2=36пјҢдё”x+y+zзҡ„жңҖеӨ§еҖјдёә7пјҢеҲҷжӯЈж•°kзӯүдәҺпјҲгҖҖгҖҖпјү
A . 1
B . 4
C . 8
D . 9
е·ІзҹҘxпјҢyвҲҲпјҲ0пјҢ+вҲһпјүпјҢиӢҘ +3
+3 пјңk
пјңk жҒ’жҲҗз«ӢпјҢеҲ©з”ЁжҹҜиҘҝдёҚзӯүејҸеҸҜжұӮеҫ—е®һж•°kзҡ„еҸ–еҖјиҢғеӣҙжҳҜ
жҒ’жҲҗз«ӢпјҢеҲ©з”ЁжҹҜиҘҝдёҚзӯүејҸеҸҜжұӮеҫ—е®һж•°kзҡ„еҸ–еҖјиҢғеӣҙжҳҜ
 +3
+3 пјңk
пјңk жҒ’жҲҗз«ӢпјҢеҲ©з”ЁжҹҜиҘҝдёҚзӯүејҸеҸҜжұӮеҫ—е®һж•°kзҡ„еҸ–еҖјиҢғеӣҙжҳҜ
жҒ’жҲҗз«ӢпјҢеҲ©з”ЁжҹҜиҘҝдёҚзӯүејҸеҸҜжұӮеҫ—е®һж•°kзҡ„еҸ–еҖјиҢғеӣҙжҳҜ
иӢҘе®һж•°aпјҢbпјҢcж»Ўи¶іa+2b+3c=2пјҢеҲҷеҪ“a2+2b2+3c2еҸ–жңҖе°ҸеҖјж—¶пјҢ2a+4b+9cзҡ„еҖјдёә
иӢҘ2x+3y+4z=11пјҢеҲҷx2+y2+z2зҡ„жңҖе°ҸеҖјдёә
и®ҫM=пјҲ  п№Ј1пјүпјҲ
п№Ј1пјүпјҲ  п№Ј1пјүпјҲ
п№Ј1пјүпјҲ  п№Ј1пјүж»Ўи¶іa+b+c=1пјҲе…¶дёӯaпјһ0пјҢbпјһ0пјҢcпјһ0пјүпјҢеҲҷMзҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲВ В пјү
п№Ј1пјүж»Ўи¶іa+b+c=1пјҲе…¶дёӯaпјһ0пјҢbпјһ0пјҢcпјһ0пјүпјҢеҲҷMзҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲВ В пјү
 п№Ј1пјүпјҲ
п№Ј1пјүпјҲ  п№Ј1пјүпјҲ
п№Ј1пјүпјҲ  п№Ј1пјүж»Ўи¶іa+b+c=1пјҲе…¶дёӯaпјһ0пјҢbпјһ0пјҢcпјһ0пјүпјҢеҲҷMзҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲВ В пјү
п№Ј1пјүж»Ўи¶іa+b+c=1пјҲе…¶дёӯaпјһ0пјҢbпјһ0пјҢcпјһ0пјүпјҢеҲҷMзҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲВ В пјү
A . [0пјҢ 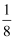 пјү
B . [
пјү
B . [ 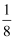 пјҢ1пјү
C . [1пјҢ8пјү
D . [8пјҢ+вҲһпјү
пјҢ1пјү
C . [1пјҢ8пјү
D . [8пјҢ+вҲһпјү
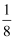 пјү
B . [
пјү
B . [ 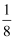 пјҢ1пјү
C . [1пјҢ8пјү
D . [8пјҢ+вҲһпјү
пјҢ1пјү
C . [1пјҢ8пјү
D . [8пјҢ+вҲһпјү
е·ІзҹҘaпјҢbвҲҲRпјҢa2+b2=4пјҢжұӮ3a+2bзҡ„еҸ–еҖјиҢғеӣҙдёәпјҲВ В пјү
A . 3a+2bвүӨ4
B . 3a+2bвүӨ  C . 3a+2bвүҘ4
D . дёҚзЎ®е®ҡ
C . 3a+2bвүҘ4
D . дёҚзЎ®е®ҡ
 C . 3a+2bвүҘ4
D . дёҚзЎ®е®ҡ
C . 3a+2bвүҘ4
D . дёҚзЎ®е®ҡ
е·ІзҹҘaпјҢbпјҢcдёәжӯЈж•°пјҢдё”a+b+c=3пјҢжұӮ  +
+  +
+  зҡ„жңҖеӨ§еҖјпјҺ
зҡ„жңҖеӨ§еҖјпјҺ
 +
+  +
+  зҡ„жңҖеӨ§еҖјпјҺ
зҡ„жңҖеӨ§еҖјпјҺ
з”Ёж•°еӯҰеҪ’зәіжі•иҜҒжҳҺдёҚзӯүејҸ1+  +
+  +вҖҰ+
+вҖҰ+  пјһ
пјһ  жҲҗз«ӢпјҢиө·е§ӢеҖјеә”еҸ–дёәn=пјҺ
жҲҗз«ӢпјҢиө·е§ӢеҖјеә”еҸ–дёәn=пјҺ
 +
+  +вҖҰ+
+вҖҰ+  пјһ
пјһ  жҲҗз«ӢпјҢиө·е§ӢеҖјеә”еҸ–дёәn=пјҺ
жҲҗз«ӢпјҢиө·е§ӢеҖјеә”еҸ–дёәn=пјҺ
и§Јзӯ”йўҳ
пјҲв… пјүжұӮеҮҪж•°fпјҲxпјү=  зҡ„жңҖеӨ§еҖјMпјҺ
зҡ„жңҖеӨ§еҖјMпјҺ
пјҲв…ЎпјүиӢҘе®һж•°aпјҢbпјҢcж»Ўи¶іa2+b2вүӨcвүӨMпјҢиҜҒжҳҺпјҡ2пјҲa+b+cпјү+1вүҘ0пјҢ并иҜҙжҳҺеҸ–зӯүжқЎд»¶пјҺ
е·ІзҹҘе…ідәҺxзҡ„дёҚзӯүејҸпјҡ|2xп№Јm|вүӨ1зҡ„ж•ҙж•°и§Јжңүдё”д»…жңүдёҖдёӘеҖјдёә2пјҺ
пјҲв… пјүжұӮж•ҙж•°mзҡ„еҖјпјӣ
пјҲв…Ўпјүе·ІзҹҘaпјҢbпјҢcвҲҲRпјҢиӢҘ4a4+4b4+4c4=mпјҢжұӮa2+b2+c2зҡ„жңҖеӨ§еҖјпјҺ
(йҖүдҝ®4-5пјҡдёҚзӯүејҸйҖүи®Іпјү
е·ІзҹҘе®һж•° 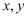 ж»Ўи¶і
ж»Ўи¶і  пјҢжұӮеҪ“
пјҢжұӮеҪ“ 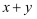 еҸ–жңҖеӨ§еҖјж—¶
еҸ–жңҖеӨ§еҖјж—¶  зҡ„еҖј.
зҡ„еҖј.
е·ІзҹҘеҮҪж•°fпјҲxпјү=m-|x-2|пјҢmвҲҲRпјҢдё”fпјҲx+2пјүвүҘ0зҡ„и§ЈйӣҶдёә[-3пјҢ3]пјҺ
-
пјҲ1пјү жұӮmзҡ„еҖјпјӣ
-
пјҲ2пјү иӢҘpпјҢqпјҢrдёәжӯЈе®һж•°пјҢдё”p+q+r=mпјҢжұӮиҜҒпјҡp2+q2+r2вүҘ3пјҺ
еҮҪж•°  зҡ„жңҖеӨ§еҖјдёәпјҺ
зҡ„жңҖеӨ§еҖјдёәпјҺ
 зҡ„жңҖеӨ§еҖјдёәпјҺ
зҡ„жңҖеӨ§еҖјдёәпјҺ
е·ІзҹҘ  жҳҜжӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„е…¬е…ұз„ҰзӮ№пјҢ
жҳҜжӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„е…¬е…ұз„ҰзӮ№пјҢ  жҳҜе®ғ们зҡ„дёҖдёӘе…¬е…ұзӮ№пјҢдё”
жҳҜе®ғ们зҡ„дёҖдёӘе…¬е…ұзӮ№пјҢдё”  пјҢи®°жӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„зҰ»еҝғзҺҮеҲҶеҲ«дёә
пјҢи®°жӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„зҰ»еҝғзҺҮеҲҶеҲ«дёә  пјҢеҲҷ
пјҢеҲҷ  зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
 жҳҜжӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„е…¬е…ұз„ҰзӮ№пјҢ
жҳҜжӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„е…¬е…ұз„ҰзӮ№пјҢ  жҳҜе®ғ们зҡ„дёҖдёӘе…¬е…ұзӮ№пјҢдё”
жҳҜе®ғ们зҡ„дёҖдёӘе…¬е…ұзӮ№пјҢдё”  пјҢи®°жӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„зҰ»еҝғзҺҮеҲҶеҲ«дёә
пјҢи®°жӨӯеңҶе’ҢеҸҢжӣІзәҝзҡ„зҰ»еҝғзҺҮеҲҶеҲ«дёә  пјҢеҲҷ
пјҢеҲҷ  зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
е·ІзҹҘжӯЈе®һж•°  пјҢ
пјҢ  пјҢ
пјҢ  ж»Ўи¶і
ж»Ўи¶і  .
.
 пјҢ
пјҢ  пјҢ
пјҢ  ж»Ўи¶і
ж»Ўи¶і  .
. иҜҒжҳҺпјҡ
-
пјҲ1пјү
 пјӣ
пјӣ
-
пјҲ2пјү
 .
.
жңҖиҝ‘жӣҙж–°
- дёӢеҲ—е…ідәҺдәҢж°§еҢ–зўізҡ„иҜҙжі•й”ҷиҜҜзҡ„жҳҜ В A.дәҢж°§еҢ–
- е»әз«Ӣе®Ңж•ҙзҡ„з”өзЈҒеңәзҗҶи®ә并йҰ–е…Ҳйў„иЁҖз”өзЈҒжіўеӯҳеңЁ
- пјҲ10зҰҸе»әзңҒзҰҸе·һ9пјҺпјүеҪ“з©әж°”еҸ—SO2дёҘйҮҚжұЎжҹ“ж—¶пјҢ
- еҰӮеӣҫжүҖзӨәзҡ„з”өи·ҜдёӯR1гҖҒR2гҖҒR4зҡҶдёәе®ҡеҖјз”өйҳ»пјҢR3
- еӣҫдёӯMгҖҒNжҳҜдёӨдёӘе…ұиҪҙеңҶзӯ’зҡ„жЁӘжҲӘйқў,еӨ–зӯ’еҚҠеҫ„дёә
- жҹҗй«ҳж ЎеңЁ2014е№ҙзҡ„иҮӘдё»жӢӣз”ҹиҖғиҜ•жҲҗз»©дёӯйҡҸжңәжҠҪ
- We suddenly saw the bus about to leave and had to run _____
- жңү关专家жҢҮеҮәпјҢдёӯеӣҪвҖ”вҖ”дёңзӣҹиҮӘз”ұиҙёжҳ“еҢәе»әжҲҗ
- 2пјҺжҲҳеӣҪжҹҗжҖқжғіе®¶и®ӨдёәпјҢеҰӮжһңдәә们дҫқйЎәеӨ©з”ҹе…·
- дёҖе№ҙ365еӨ©пјҢйҷӨдәҶе№ҙеҲқејҖдәәд»Јдјҡзҡ„еҮ еӨ©пјҢе…¶дҪҷж—¶
- дёӢеӣҫдёәжҹҗж—Ҙжҹҗж—¶еҲ»еҚҠзҗғжҳјеӨңеҲҶеёғзӨәж„ҸеӣҫпјҢйҳҙеҪұ
- My uncle sang a few old songs, my aunt ________ the piano t
- дёӢеҲ—еҗ„з»„еҢ–еҗҲзү©дёӯпјҢе…ЁжҳҜеҶ…зҺҜеўғжҲҗеҲҶзҡ„дёҖз»„жҳҜ
- жҠӣзү©зәҝy=(mпјҚ4)x2пјҚ2mxпјҚmпјҚ6зҡ„йЎ¶зӮ№еңЁxиҪҙдёҠпјҢеҲҷm
- DAPжҳҜз”өеҷЁе’Ңд»ӘиЎЁдёӯеёёз”Ёзҡ„дёҖз§Қй«ҳеҲҶеӯҗеҢ–еҗҲзү©пјҢ
- дёӢеҲ—еӣӣз§Қж ёиӢ·й…ёдёӯпјҢиғҪеңЁATPдёӯжүҫеҲ°зҡ„жҳҜ AпјҺВ B
- вҖ” What a fine day! Shall we go shopping? вҖ” ________пјҺBu
- зҡ„еұ•ејҖејҸдёӯзҡ„еёёж•°йЎ№дёә A. 12В В В В В В В В В В B
- з»ҶиғһдёӯжңҖйҮҚиҰҒзҡ„з»“жһ„жҳҜпјҲпјү В В AгҖҒз»ҶиғһеЈҒВ В В
- дёӢеҲ—еҸҘеӯҗдёӯжІЎжңүиҜӯз—…зҡ„дёҖеҸҘжҳҜ AпјҺзӣӣеӨҸж—¶иҠӮзҡ„



