二维形式的柯西不等式 知识点题库
已知x , y>0,且xy=1 ,则 的最小值为( )
的最小值为( )
 的最小值为( )
的最小值为( )
A . 4
B . 2
C . 1
D . 

已知 ,x , y>0,则x+y的最小值是( )
,x , y>0,则x+y的最小值是( )
 ,x , y>0,则x+y的最小值是( )
,x , y>0,则x+y的最小值是( )
A .  B .
B .  C .
C . 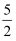 D . 5
D . 5
 B .
B .  C .
C . 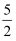 D . 5
D . 5
已知x+y=1,那么 2x2+3y2 的最小值是( )
A . 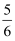 B .
B .  C .
C .  D .
D . 
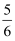 B .
B .  C .
C .  D .
D . 
若a+b=1,则 的最小值为( )
的最小值为( )
 的最小值为( )
的最小值为( )
A . 1
B . 2
C .  D .
D . 
 D .
D . 
已知x,y,z,a∈R,且x2+4y2+z2=6,则使不等式x+2y+3z≤a恒成立的a的最小值为( )
A . 6
B .  C . 8
D .
C . 8
D . 
 C . 8
D .
C . 8
D . 
已知x,y,z,a,b,c,k均为正数,且x2+y2+z2=10,a2+b2+c2=90,ax+by+cz=30,a+b+c=k(x+y+z),则k=( )
A .  B .
B .  C . 3
D . 9
C . 3
D . 9
 B .
B .  C . 3
D . 9
C . 3
D . 9
设a,b∈R+ , a+b=1,则 +
+ 的最小值为( )
的最小值为( )
 +
+ 的最小值为( )
的最小值为( )
A . 2+ B . 2
B . 2 C . 3
D .
C . 3
D . 
 B . 2
B . 2 C . 3
D .
C . 3
D . 
设函数f(x)= +
+ 的最大值为M.
的最大值为M.
 +
+ 的最大值为M.
的最大值为M.(Ⅰ)求实数M的值;
(Ⅱ)求关于x的不等式|x﹣1|+|x+2|≤M的解集.
(1)证明柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2;
(2)若a,b∈R+且a+b=1,用柯西不等式求 +
+ 的最大值.
的最大值.
已知θ∈(  ,
,  ),若存在实数x,y同时满足
),若存在实数x,y同时满足  =
=  ,
,  +
+  =
=  ,则tanθ的值为.
,则tanθ的值为.
 ,
,  ),若存在实数x,y同时满足
),若存在实数x,y同时满足  =
=  ,
,  +
+  =
=  ,则tanθ的值为.
,则tanθ的值为.
二维形式的柯西不等式可用( )表示.
A . a2+b2≥2ab(a,b∈R)
B . (a2+b2)(c2+d2)≥(ab+cd)2(a,b,c,d∈R)
C . (a2+b2)(c2+d2)≥(ac+bd)2(a,b,c,d∈R)
D . (a2+b2)(c2+d2)≤(ac+bd)2(a,b,c,d∈R)
[选修4-5:不等式选讲]
已知a>0,b>0,a3+b3=2,证明:
已知a>0,b>0,a3+b3=2,证明:
(Ⅰ)(a+b)(a5+b5)≥4;
(Ⅱ)a+b≤2.
已知关于  的不等式
的不等式  有解。
有解。
 的不等式
的不等式  有解。
有解。(I)求实数  的取值范围;
的取值范围;
(II)已知  ,证明:
,证明:  。
。
“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即  )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数  的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
 )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数  的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知实数x,y满足  则
则  的最大值为.
的最大值为.
 则
则  的最大值为.
的最大值为.
已知椭圆  和双曲线
和双曲线  有相同焦点
有相同焦点  ,且它们的离心率分别为
,且它们的离心率分别为  ,设点
,设点  是
是  与
与  的一个公共点,若
的一个公共点,若  ,则
,则  的最小值为.
的最小值为.
 和双曲线
和双曲线  有相同焦点
有相同焦点  ,且它们的离心率分别为
,且它们的离心率分别为  ,设点
,设点  是
是  与
与  的一个公共点,若
的一个公共点,若  ,则
,则  的最小值为.
的最小值为.
已知函数f(x)=|x-2|+|x+1|.
-
(1) 解不等式f(x)>x+2;
-
(2) 记f(x)的最小值为m,正实数a,b,c满足a+b+c=m,证明:

已知  是正实数,且满足
是正实数,且满足  .
.
 是正实数,且满足
是正实数,且满足  .
.
-
(1) 是否存在满足已知条件的
 ,使得
,使得  ,试说明理由;
,试说明理由;
-
(2) 求
 的最大值.
的最大值.
已知实数  ,
,  ,
,  满足
满足  ,且
,且  ,则下列结论正确的是( )
,则下列结论正确的是( )
 ,
,  ,
,  满足
满足  ,且
,且  ,则下列结论正确的是( )
,则下列结论正确的是( )
A .  的最小值为
的最小值为  B .
B .  的最大值为
的最大值为  C .
C .  的最小值为
的最小值为  D .
D .  取最小值时
取最小值时 
 的最小值为
的最小值为  B .
B .  的最大值为
的最大值为  C .
C .  的最小值为
的最小值为  D .
D .  取最小值时
取最小值时 
已知函数

-
(1) 解不等式:
 ;
;
-
(2) 记
 的最小值为
的最小值为 , 若
, 若 , 且
, 且 , 证明:
, 证明:
最近更新
- 某学习小组利用如图仪器或装置进行气体制备
- 下列各句中“也”的意义和用法不同的一项是
- 已知:2H2(g)+O2(g)=2H2O (g) △H1 3H2(g)+Fe
- 春蚕到死丝方尽,_______________________。(李商隐
- 广西壮族自治区卫生厅于2010年五月中旬了20lO
- 2008年5月12日14时28分四川汶川发生8.0级地震,
- 下列关于选择透过性膜和半透膜的关系,正确
- 下列有关ATP的叙述,正确的是( ) A.线粒体是
- 坦克有宽宽的履带,可以减小 ;小
- 如图所示,两通电细直导线竖直放置,所通电
- 如图所示,斜面体固定在水平面上,小物块A
- A child who has once been pleased with a tale likes, as a ru
- 文化产业的良好发展离不开健康的文化市场,
- 按照三大类岩石划分,玄武岩属于 �
- 如图3-7-7所示,浸在水的小球的密度小于水中
- 17. .阅读下列新闻材料,按照题目要求作答。
- 下列有关胶体的说法不正确的是( ) A. 分
- 在下面的空格处填上课文中的相关语句。 鲁
- Let's have a break. A. have supper B. have a r
- 新农保要求中央确定基本原则和主要政策,地



