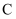扇形统计图 知识点题库
某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在该被调查的学生中,跑步和打羽毛球的学生人数分别是( )

A . 30,40
B . 45,60
C . 30,60
D . 45,40
某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.

-
(1) 样本中最喜欢A项目的人数所占的百分比为,其所在扇形统计图中对应的圆心角度数是度;
-
(2) 请把条形统计图补充完整;
-
(3) 若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.

-
(1) 求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
-
(2) 该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:

-
(1) 本次比赛参赛选手共有人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为;
-
(2) 赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
-
(3) 成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
红星小学对全校同学进行最喜欢的运动项目调查,调查情况具体如图,其中150名同学喜欢羽毛球,喜欢跳绳的同学有多少名?

某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:

-
(1) 求本次测试共调查了多少名学生?
-
(2) 求本次测试结果为B等级的学生数,并补全条形统计图;
-
(3) 请你计算扇形统计图中八年级学生体能测试结果为D等级的扇形圆心角的度数.
目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,八年级数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如下不完整的统计图.

-
(1) m=,n=.
-
(2) 将这两个统计图补全.
-
(3) 根据抽样调查的结果,请估算全校2000名学生中大约有多少人最认可“微信”这一新生事物?
-
(4) 已知A,B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”,从这四名同学中抽取两名同学,请你通过列表或画树状图的方法求出这两位同学最认可的新生事物不一样的概率.
课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A-优秀,B-良好,C一般,D-较差,并将调查结果绘制成以下两幅不完整的统计图。请你根据统计图,解答下列问题:

-
(1) 本次一共调查了多少名学生?
-
(2) C类女生有名,D类男生有名,并将条形统计图补充完整;
-
(3) 若从被调查的A类和C类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树状图的方法求出所选同学中恰好是一位男同学和一位女同学的概率。
2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化.某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图.请你根据图中提供的信息完成下列问题:

-
(1) 求被调查学生的人数,并将条形统计图补充完整;
-
(2) 求扇形统计图中的A等对应的扇形圆心角的度数;
-
(3) 已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?
一次防流感知识检测中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次检测中甲、乙两组学生人数相同,成绩如下两个统计图:

-
(1) 在乙组学生成绩统计图中,8分所在的扇形的圆心角为度;
-
(2) 请列式计算乙组平均分,补充完整下面的成绩统计分析表所有空格:
平均分
方差
众数
中位数
优秀率
甲组
7
1.8
7
7
20%
乙组
2.6
10%
-
(3) 甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
某校学生到校方式情况的扇形统计图如图所示,若该校步行到校的学生有200人,则乘公共汽车到校的学生有人.

我省某地区结合本地自然条件,大力发展茶叶、蔗糖、水果、药材等产业,取得良好经济效益,茶叶、蔗糖、水果、药材成了该地区四大产业,图①、图②是根据该地区2010年各项产业统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息答下列问题:

-
(1) 该地区2010年各项产业总值共万元;
-
(2) 图①中蔗糖所点的百分数是,2010年该地区蔗糖业的产值有万元;
-
(3) 将图②中“蔗糖”部分的图形补充完整.
某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
|
组别 |
符合题意字数 | 人数 |
| | | 10 |
| | | 15 |
| | | 25 |
| | | |
| | | |

根据以上信息解决下列问题:
-
(1) 在统计表中,
 ,
, 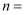 _;并补全条形统计图.
_;并补全条形统计图.
-
(2) 扇形统计图中“
 组”所对应的圆心角的度数_;
组”所对应的圆心角的度数_;
-
(3) 若该校共有9000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
某社区为了加强社区居民对新型冠状病毒感染的肺炎的防护知识的学习,在微信群进行了线上防护知识测试,且设立一等奖、二等奖、三等奖三个奖项,并绘制了如下不完整的统计图,则一等奖的获奖人数为( )


A . 10
B . 8
C . 7
D . 6
近期,锦江区各学校开展了“近视防控”系列活动,以此培养学生良好用眼习惯,降低近视发病率.为了了解学生对于“近视防控”知识的掌握程度,某学校采用随机抽样的调查方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

-
(1) 请补全条形统计图;扇形统计图中“合格”部分所对应扇形的圆心角的大小为 ;
-
(2) 若该学校共有学生800人,请根据上述调查结果,估计该学校学生中“近视防控”知识掌握程度为“良好”的人数;
-
(3) 若从对“近视防控”知识掌握程度为“优秀”的3个女生和1个男生中随机抽取2人,为“待合格”的同学进行“近视防控”知识宣讲,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
为弘扬中华传统文化,感受中华诗词的独特魅力,校团委会举办首届“校园诗词大会”,初赛共10道题,每题10分,王敏从初赛名单中随机抽取部分同学的成绩,绘制出如下的统计图(1)和图(2).请根据相关信息,解答下列问题:

-
(1) 图(1)a的值为 ▲ , 补全条形统计图;
-
(2) 求被抽取的初赛成绩的平均数,众数和中位数;
-
(3) 如果初赛成绩在90分或90分以上的同学进入复赛,请估计参加初赛的160位同学中有多少同学可以参加复赛.
某中学对全校九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给信息,解答下列问题:

第18题图
-
(1) 将条形统计图补充完整;
-
(2) 在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是度;
-
(3) 学校九年级共有600人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩类别可以达到“中”(不包括“中” ) 以上?
-
(4) 学校准备从成绩进步最大的3名同学(1名男生、2名女生)中随机选取2名同学介绍学习经验,则选出的同学恰好是2名女生的概率是 .
2021年7月24 日,教育部官网正式发布由中共中央办公厅,国务院办公厅印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.秋季开学后,某市教育主管部门为了了解学校"减轻学生作业负担"情况,在甲和乙两所初级中学中各随机抽查了50名学生完成书面作业所用的时间,并绘制了如下统计图表∶

根据以上图表信息回答下列问题∶
-
(1) 统计表中m=,n=;
-
(2) 乙学校在调查的 50名学生中,需要 90分钟以上才能完成书面作业的有人;
-
(3) 设a为甲学校抽取的 50名学生完成书面作业时间的中位数,b为乙学校抽取的50名学生完成书面作业时间的中位数,则ab.(填“>”或“=”或“<”)
-
(4) 若该市有初中在校生15000人.根据对甲、乙两所学校调查的情况.估计能在国家规定的90分钟(含90分钟)内完成书面作业的人数.
每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
八年级抽取的学生的竞赛成绩:
4,10,8,6,6,6,7,7,7,6,9,9,8,8,8,8,8,9,10,4.
|
七年级抽取的学生的竞赛成绩条形统计图
|
七、八年级抽取的学生的竞赛成绩统计表
|
根据以上信息,解答下列问题:
-
(1) 填空:a=,b=,c=;
-
(2) 估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;
-
(3) 根据以上数据分析,你认为该校哪个年级“国家安全法”知识竞赛的学生成绩更优异?请说明理由.
近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其它,该小组对某超市一天内购物者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
-
(1) 本次一共调查了多少名购物者?
-
(2) 请补全条形统计图;在扇形统计图中C种支付方式所对应的圆心角为 ▲ 度.
-
(3) 若该超市这一周内有2200名购物者,请估计使用A和B两种支付方式的购物者约有多少名?
最近更新
- 现有下列高聚物:A.聚乙烯 B.天然橡胶树脂
- 下列命题:(1)钝角是第二象限的角,(2)
- (6分)某有机物0.3克完全燃烧后生成224毫升
- 16.在下面一段文字横线处补写恰当的语句,
- A、B、C为初中化学常见物质,它们之间的转化
- 跳虫、甲螨和线虫是土壤中的主要动物类群
- I am leaving my ________ position because I cannot show my c
- 右图为氯化钠、碳酸钠在水中的溶解度曲线。
- 文学常识与名篇填空。(5题限选4题) (1)
- 表面积为 的正八面体的各个顶点都在同一个
- 常温下,下列溶液的pH或微粒的物质的量浓度
- 1.下列句中划线词的解释不正确的一项是 A.
- 下列选项属于物质范畴的是( ) ①人脑 �
- 读河流平面、剖面图,回答下列问题。 (1)填
- 已知命题p :x∈(0,),使得cos x≥x,则该命题
- 宋庆龄说:“孙中山和中国共产党之
- 如图所示,三个小球从同一高处的点分别以水
- 人们通常根据文献资料研究历史,而今以口述
- 如图所示,一轻质弹簧两端分别与竖直墙壁和
- She was afraid __________ the dog in case it became dangerou