异面直线 知识点题库
如图S为正三角形ABC所在平面外一点,且SA=SB=SC=AB,E、F分别为SC、AB中点,则异面直线EF与AC所成角为( )

A . 60º
B . 90º
C . 45º
D . 30º
将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线MN与PQ是异面直线的是( )
C
① ② ③ ④
A . ①②
B . ②④
C . ①④
D . ①③
如图,正方体ABCD﹣A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.
(Ⅰ)用向量方法求直线EF与MN的夹角;
(Ⅱ)求二面角N﹣EF﹣M的平面角的正切值.

如图,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∉直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )

A . 当|CD|=2|AB|时,M,N两点不可能重合
B . M,N两点可能重合,但此时直线AC与直线l不可能相交
C . 当AB与CD相交,直线AC平行于l时,直线BD可以与l相交
D . 当AB,CD是异面直线时,MN可能与l平行
如图,在直三棱柱  中,
中,  ,
,  为棱
为棱  的中点,
的中点,  .
.
 中,
中,  ,
,  为棱
为棱  的中点,
的中点,  .
.
-
(1) 证明:
 平面
平面  ;
;
-
(2) 设二面角
 的正切值为
的正切值为  ,
,  ,
,  ,求异面直线
,求异面直线  与
与 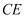 所成角的余弦值.
所成角的余弦值.
如图,在三棱柱  中,
中,  底面
底面  ,
,  是
是  的中点,
的中点,  ,
,  ,过点
,过点  、
、  作截面交
作截面交  于点
于点  ,若点
,若点  恰好是
恰好是  的中点,则直线
的中点,则直线  与
与  所成角的余弦值为.
所成角的余弦值为.
 中,
中,  底面
底面  ,
,  是
是  的中点,
的中点,  ,
,  ,过点
,过点  、
、  作截面交
作截面交  于点
于点  ,若点
,若点  恰好是
恰好是  的中点,则直线
的中点,则直线  与
与  所成角的余弦值为.
所成角的余弦值为.
矩形ABCD中,  ,
, 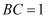 ,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
 ,
, 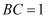 ,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,如图,已知正三棱柱  的各条棱都相等,M是侧棱
的各条棱都相等,M是侧棱  的中点,则异面直线
的中点,则异面直线  和
和  所成角的大小是( )
所成角的大小是( )
 的各条棱都相等,M是侧棱
的各条棱都相等,M是侧棱  的中点,则异面直线
的中点,则异面直线  和
和  所成角的大小是( )
所成角的大小是( )
A .  B .
B .  C .
C .  D .
D . 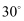
 B .
B .  C .
C .  D .
D . 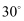
四边形  和
和  均为正方形,它们所在的平面互相垂直,则异面直线
均为正方形,它们所在的平面互相垂直,则异面直线  与
与  所成的角为( )
所成的角为( )
 和
和  均为正方形,它们所在的平面互相垂直,则异面直线
均为正方形,它们所在的平面互相垂直,则异面直线  与
与  所成的角为( )
所成的角为( )
A .  B .
B .  C .
C .  D .
D . 
如图,已知  分别是正方形
分别是正方形  的边
的边  的中点,现将正方形沿
的中点,现将正方形沿  折成
折成  的二面角,则异面直线
的二面角,则异面直线  与
与 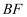 所成角的余弦值是.
所成角的余弦值是.
 分别是正方形
分别是正方形  的边
的边  的中点,现将正方形沿
的中点,现将正方形沿  折成
折成  的二面角,则异面直线
的二面角,则异面直线  与
与 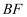 所成角的余弦值是.
所成角的余弦值是. 
如图,在四面体  中,
中,  平面
平面  ,面
,面  面
面  .
.
 中,
中,  平面
平面  ,面
,面  面
面  .
. 
-
(1) 求证:
 平面
平面  ;
;
-
(2) 若
 ,
, 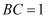 ,求异面直线
,求异面直线  与
与  所成角的正弦值.
所成角的正弦值.
正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为.
已知异面直线a , b分别在平面α , β内,且α∩β=c , 那么直线c一定( )
A . 与a , b都相交
B . 只能与a , b中的一条相交
C . 至少与a , b中的一条相交
D . 与a , b都平行
三棱锥  中,
中,  两两垂直且相等,点
两两垂直且相等,点  ,
,  分别是
分别是  和
和  上的动点,且满足
上的动点,且满足  ,
,  ,则
,则  和
和  所成角余弦值的取值范围是.
所成角余弦值的取值范围是.
 中,
中,  两两垂直且相等,点
两两垂直且相等,点  ,
,  分别是
分别是  和
和  上的动点,且满足
上的动点,且满足  ,
,  ,则
,则  和
和  所成角余弦值的取值范围是.
所成角余弦值的取值范围是.
如图,  分别是正三棱柱的顶点或所在棱的中点,则直线
分别是正三棱柱的顶点或所在棱的中点,则直线  是异面直线的图形有.(填序号)
是异面直线的图形有.(填序号)
 分别是正三棱柱的顶点或所在棱的中点,则直线
分别是正三棱柱的顶点或所在棱的中点,则直线  是异面直线的图形有.(填序号)
是异面直线的图形有.(填序号) 
如图是正方体的平面张开图,在这个正方体中:

①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°;
④DM与BN是异面直线;
以上四个命题中,正确命题的序号是.
如图所示,已知正三棱柱ABC﹣A1B1C1 的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )

A . 60°
B . 45°
C . 90°
D . 30°
已知  ,
,  分别是直线
分别是直线  ,
,  的方向向量,那么“
的方向向量,那么“  ,
,  不平行”是“
不平行”是“  ,
,  异面”的( )
异面”的( )
 ,
,  分别是直线
分别是直线  ,
,  的方向向量,那么“
的方向向量,那么“  ,
,  不平行”是“
不平行”是“  ,
,  异面”的( )
异面”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
在空间直角坐标系  中,已知点
中,已知点  ,
,  ,
,  ,则平面
,则平面  的一个法向量
的一个法向量  ,异面直线
,异面直线  与
与  所成角的余弦值为.
所成角的余弦值为.
 中,已知点
中,已知点  ,
,  ,
,  ,则平面
,则平面  的一个法向量
的一个法向量  ,异面直线
,异面直线  与
与  所成角的余弦值为.
所成角的余弦值为.
如图,在单位正方体 中,点P是线段
中,点P是线段 上的动点,给出以下四个命题:
上的动点,给出以下四个命题:
 中,点P是线段
中,点P是线段 上的动点,给出以下四个命题:
上的动点,给出以下四个命题:
①异面直线 与直线
与直线 所成角的大小为定值;②二面角
所成角的大小为定值;②二面角 的大小为定值;③若Q是对角线
的大小为定值;③若Q是对角线 上一点,则
上一点,则 长度的最小值为
长度的最小值为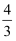 ;④若R是线段
;④若R是线段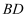 上一动点,则直线PR与直线
上一动点,则直线PR与直线 不可能平行.
不可能平行.
其中真命题有( )
A . 1个
B . 2个
C . 3个
D . 4个
最近更新
- 近年来,江苏省的电子政务建设步伐明显加快,国家电子政务内网成功落地,全省电子政务内网已覆盖所有省级党政军部门、中央在苏单
- 下列关于催化剂的说法中,正确的是 A. 催化剂能改变化学反应速率 B. 催化剂在反应后质量会减少 C. 催化剂在反应后化
- 2012年,第30届奥运会将在伦敦举行,这个世界体坛盛会起源于古代的希腊。据说古奥运会是为祭祀宙斯神而举办的,运动会期间
- 【江苏南通】对有关实验现象的描述正确的是A.碳在氧气中燃烧放出白烟牋牋牋牋牋牋
- Ben likes swimming very much, but he _______running. A.
- 已知Cl—、Fe2+、I—、SO2均具有还原性,且在酸性溶液中的还原性依次增强,下列各反应不可能发生的是( )A.
- 新闻点评就是用简约的文字对新闻进行评论,请点评下面一则新闻。要求观点鲜明,语言准确、生动,不超过30字。 2月22日,南
- 从身边的小事做起,节约每一张纸、一度电、一滴水、一滴油、一粒米、一块煤……如果人人都节约资源意识渗透至生活中每一个细节,
- 有总物质的量一定的甲烷和某有机物A(分子式为CaHbOc,a≥1、c≥1、b为正整数)的混合物。 (1)若混合物中甲烷和
- ----Have you moved into your new flat?----No, I haven’t. It
- 2014年9月17日,国家质检总局,公布了包括广州市奥博文具有限公司、东莞市智高文具有限公司、亚龙纸制品(昆山)有限公司
- With both hands resting on top of the steering wheel, Oshima
- 下列图示的装置不属于原电池的是
- The disabled young man believes that his dream to get his no
- 如图1,不是轴对称图形的是( ) 图1
- 已知A 是一种分子量为28的气态烃,现以A为主要原料合成一种具有果香味的物质E,其合成路线如下图所示。请回答下列问题:
- 关于科学家和他们的贡献,下列说法中正确的是 A.安培首先发现了电流的磁效应 B.伽利略认为自由落体运动是速度随位移均匀变
- 某个体户到农贸市场进一批黄瓜,卖掉后还剩48kg,则该个体户卖掉______kg黄瓜.
- 用所给单词的适当形式填空1. His father________(work) in that factory,but
- 根据实验判断下列说法错误的是 A.该固体物质的溶解度随温度的升高而增大 B.溶液b一定是不饱和溶液



