一元二次方程的应用 知识点题库

广州亚运会期间，某纪念品原价168元，连续两次降价a%后售价为128元，下列所列方程正确的是（　　）

文峰千家惠四月份的利润是25万元，预计六月份的利润将达到36万元，设平均每月增长的百分率为x，根据题意所列方程正确的是（    ）．

汽车刹车后行驶的距离s（单位：米）与行驶的时间t（单位：秒）的函数关系式是s=15t-6t² ， 那么汽车刹车后几秒停下来？（　　）

根据下列问题，列出关于x的方程，并将其化成一元二次方程的一般形式．

一个两位数，个位上的数字比十位上的数字小4，且个位上数字与十位上数字的平方和比这个两位数小4，求这个两位数．

一海关缉私艇发现在正北方45海里处有一艘可疑船只，测得它以60海里/时的速度向正东方向航行，立即调整方向，以75海里/时的速度准备将其拦截，问经过多少时间能拦截上？

泰兴鑫都小商品市场以每副60元的价格购进800副羽毛球拍．九月份以单价100元销售，售出了200副．十月份如果销售单价不变，预计仍可售出200副，鑫都小商品市场为增加销售量，决定降价销售，根据市场调查，销售单价每降低5元，可多售出10副，但最低销售单价应高于购进的价格．十月份结束后，批发商将对剩余的羽毛球拍一次性清仓，清仓时销售单价为50元．设十月份销售单价降低x元．

（1）填表：

月份	九月	十月	清仓
销售单价（元）	100		50
销售量（件）	200

（2）如果鑫都小商品市场希望通过销售这批羽毛球拍获利9200元，那么十月份的销售单价应是多少元？

下列方程中，有实数解的是（　　）

刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对（a，b）进入其中时，会得到一个新的实数：a²+b﹣1，例如：把（3，﹣2）放入其中，就会得到3²+（﹣2）﹣1=6．现将实数对（m，﹣2m）放入其中，得到实数2，则m的值是（　　）

方程=x﹣1的根是 

某超市一月份的营业额为30万元，三月份的营业额为56万元．设每月的平均增长率为x，则可列方程为（  ）

为满足社区居民健身的需要，市政府准备采购若干套健身器材免费提供给社区，经考察，劲松公司有A，B两种型号的健身器材可供选择．

为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系：y＝－2x＋80.设这种产品每天的销售利润为w元．

若一元二次方程ax²=b（ab＞0）的两个根分别是m+1与2m﹣4，则 =．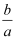

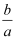某校九年级学生毕业时，每个同学都将自己的相片向全班其他同学各送一张作纪念，全班共送了2070张相片．若全班有x名学生，根据题意，列出方程为．

如图，直角坐标系xoy中，四边形ODEF和四边形ABCD都是正方形，点F在x轴的正半轴上，点C在边DE上，反比例函数 （k≠0，x＞0）的图象过点B，E.若AB=2，则正方形ODEF的边长为.

请阅读下面材料：

问题：已知方程x²+x-3＝0，求一个一元二次方程，使它的根分别是已知方程根的一半．

解：设所求方程的根为y，y= ，所以x＝2y

把x＝2y代入已知方程，得(2y)²+2y-3＝0

化简，得4y²+2y-3＝0

故所求方程为4y²+2y-3＝0

这种利用方程根的代换求新方程的方法，我们称为“换根法”．请用阅读材料提供的“换根法”解决下列问题：

2020年12月25日，太原市地铁2号线一期线路正式投入载客初期运营，历时四年9个月的建设后，太原人终于能乘坐自己的地铁了．在2号线轨道铺设作业中，为了提前完成铺轨任务，采用了新型轮胎式铺轨机和全自动混凝土布料机，使得每天铺设轨道的长度比原计划多120米，原计划300天的铺轨任务，仅用了120天就全部完成．

图1

《九章算术》是我国古代的数学名著，其中“勾股”章有一题，大意是说：已知矩形门的高比宽多 尺，门的对角线长 尺，那么门的高和宽各是多少?如果设门的宽为 尺，根据题意，那么可列方程．

某校九年级举行篮球赛（每两班比赛一场），共比赛了15场，则九年级共有个班.

某厂家1~5月份的口罩产量统计如图所示，设从2月份到4月份，该厂家口罩产量的平均月增长率为x，则根据题意可列方程为（   ）