八年级(初二)试题

[图片展览]

漫画一 漫画二 漫画三
[法律宣传]
2021年12月24日,第十三届全国人民代表大会常务委员会第三十二次会议通过《中华人民共和国反有组织犯罪法》。该法第一条规定,为了预防和惩治有组织犯罪,加强和规范反有组织犯罪工作,维护国家安全、社会秩序、经济秩序,保护公民和组织的合法权益,根据宪法,制定本法。
[建言献策]
2022年3月5日,李克强总理在政府工作报告中指出,政府工作存在不足,形式主义、官僚主义仍然突出,脱离实际、违背群众意愿现象屡有发生,有的在政策执行中采取“一刀切”、运动式做法。少数干部不担当、不作为、乱作为,有的漠视严重侵害群众权益问题、工作严重失职失责。一些领域腐败问题依然多发。
-
(1) 我国宪法明确规定:“国家尊重和保障人权。”请写出上述三幅漫画所体现的人权内容。
-
(2) 结合上述材料谈谈宪法与反有组织犯罪法之间的关系?
-
(3) 结合上述材料谈谈,如何规范权力运行,以解决政府工作中的上述存在问题?
 切
切  于点
于点  ,点
,点  在
在  上,且
上,且  ,连结
,连结  并延长交
并延长交  于点
于点  ,
,  的半径为2,设
的半径为2,设  ,
,  当
当  时,
时,  是等腰直角三角形;
是等腰直角三角形;  若
若  ,则
,则  ;
;  当
当  时,
时,  与
与  相切.以上选项正确的有( )
相切.以上选项正确的有( )

 B .
B .  C .
C .  D .
D . 
 B . 迪亚士
B . 迪亚士  C . 达·伽马
C . 达·伽马  D . 麦哲伦
D . 麦哲伦 
满铁范为一板 则以一铁范置铁板上
不以木为之者 则以纸帖之
| 年份 | 拥有厂家 | 拥有资本 | 工人人数 |
| 1913年 | 689家 | 33亿元 | 27万多 |
| 1920年 | 1795家 | 50亿元 | 55万多 |
在边长为5的正方形ABCD中,点E,F分别是BC,DC边上的两个动点(不与点B,C,D重合),且AE⊥EF.

-
(1) 如图1,当BE=2时,求FC的长;
-
(2) 延长EF交正方形ABCD外角平分线CP于点P.
①依题意将图2补全;
②小京通过观察、实验提出猜想:在点E运动的过程中,始终有AE=PE.小京把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的三种想法:
想法1:在AB上截取AG=EC,连接EG,要证AE=PE,需证△AGE≌△ECP.
想法2:作点A关于BC的对称点H,连接BH,CH,EH.要证AE=PE,需证△EHP为等腰三角形.
想法3:将线段BE绕点B顺时针旋转90°,得到线段BM,连接CM,EM,要证AE=PE,需证四边形MCPE为平行四边形.
请你参考上面的想法,帮助小京证明AE=PE.(一种方法即可)
-
(1) 生物学家根据生物之间的相似程度,把生物划分为7个不同的等级,其中最基本的分类单位是.
-
(2) 根据动物体内有无,动物可分为无脊椎动物和脊椎动物两大类.
-
(3)
请从“藻类植物、被子植物、单子叶植物、肾蕨、马尾松”中选三种名称填在下面对应的方框①、②、③中,完善有关植物分类的概念图.


 中,
中,  ,
,  .过点
.过点  作射线
作射线  ,点 M,、N分别在边
,点 M,、N分别在边  、
、  上(点
上(点  、
、  不与所在线段端点重合),且
不与所在线段端点重合),且  ,连结
,连结  并延长交
并延长交  于点
于点  ,连结
,连结  并延长交
并延长交  的垂直平分线于点
的垂直平分线于点  ,连结
,连结 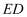 .
. 
-
(1) 【猜想】如图①,当
 时,可证
时,可证  .从而得出
.从而得出  ,进而得出
,进而得出 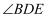 的大小为多少度.
的大小为多少度.
-
(2) 【探究】如图②,若
 .
. Ⅰ.求证:
 .
.Ⅱ.
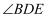 的大小为多少度(用含
的大小为多少度(用含  的代数式表示)
的代数式表示) -
(3) 【应用】如图③,当
 时,连结
时,连结  .若
.若 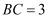 ,
,  ,则
,则  的面积为多少.
的面积为多少.
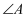 的度数为( )
的度数为( ) 
 是关于
是关于 的多项式.请写出多项式
的多项式.请写出多项式 , 并将该例题的解答过程补充完整.
, 并将该例题的解答过程补充完整.例先去括号,再合并同类项: 解:
|
- 下列关于电磁波的叙述中,正确的是( ) A.电磁波是电磁场由发生区域向远处的传播 B.电磁波在任何介质中传播速度均
- 下列不属于酶的固定方式的是 A.将酶包埋在细微网格中 B.将酶相互连接起来 C.将酶吸附在载体表面
- 上古时期,河水泛滥成灾,因而,也就出现了一个治水的英雄是( ) A、尧 B、禹
- 在社会主义社会,国民收入的分配不能由人们的主观愿望决定,而是要受客观经济条件的制约。据此回答问题。 国民收入经过复杂的分
- 1.依次填入下列各句横线处的词语,最恰当的一组是( ) ①锦袋内掣出那管凤箫,李师师接来,口中轻轻吹动,端的是之声。
- 下列说法中正确的是 A.钢、青铜、硬铝和金刚石都是合金材料 B.所有的分解反应都属于氧化还原反应
- 让钢琴和手风琴都发出C调的“do”,我们能区分开是钢琴还是手风琴的声音,这是依据
- 据史料记载:1851年,英国总人口为2780万人,其中城市人口占英国总人口的50.2%,首次超过了乡村人口。导致这种现象
- 双曲线的两条准线把两焦点所连线段三等分,则它的离心率为()A. B.
- 下列文常表达有误的一项是 ( ) A.“街上的柳树,像病了似的,叶子挂着层灰土在枝上打着卷;枝条一动也懒
- 已知电极上每通过96 500 C的电量就会有1 mol电子发生转移。精确测量金属离子在惰性电极上以镀层形式沉积的金属质量
- 从结构层次上看,人比植物更复杂一些,这主要是由于() A. 植物的组织种类少 B. 人是由受精卵发育而来的
- 下列元素中不属于主族元素的是 A. 磷 B. 铁 C. 碘
- 今年秋天,山东曲阜的一家葡萄种植专业户,由于种植面积大、产量高,而销路窄,致使大量的葡萄堆积腐烂。其相邻的一家养猪专业户
- 一火箭喷气发动机每次喷出m=200 g的气体,喷出的气体相对地面的速度v=1 000 m/s.设此火箭初始质量M=300
- 大气中氧气和二氧化碳的含量能保持相对稳定,是由于( ) A.光合作用的结果
- 列宁说:“目前的新事物,就是我国革命在经济建设的一些根本问题上必须采取‘改良主义的、渐进主义的、审慎迂回的行动方式’。”
- Books are made __________ paper while paper is mainly made _
- 如图,圆O的半径OB垂直于直径AC,M为OA上一点,BM的延长线交圆O于N,过N点的切线交CA的延长线于P。(1)求证
- Does John know any other foreign language ___French? A. exce
 .
. 
 .
.


