复合场 知识点题库
有一匀强电场,其场强为E,方向水平向右,把一个半径为r的光滑绝缘环,竖直放置于场中,环面平行于电场线,环的顶点A穿有一个质量为m,电量为q(q>0)的空心小球,如图所示,当小球由静止开始从A点下滑1/4圆周到B点时,小球对环的压力大小为( )
A . 2mg
B . qE
C . 2mg+qE
D . 2mg+3qE
在赤道处,将一小球向东水平抛出,落地点为A;给小球带上电荷后,仍以原来的速度抛出,考虑地磁场的影响,下列说法正确的是( )
A . 无论小球带何种电荷,小球仍会落在A点
B . 无论小球带何种电荷,小球下落时间都会延长
C . 若小球带负电荷,小球会落在更远的B点
D . 若小球带正电荷,小球会落在更远的B点
地面附近空间存在水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,电场方向水平向右,一个带电油滴能沿一条与竖直方向成θ的直线MN运动(MN在竖直平面内),如图所示,则以下判断正确的是
A . 可能是带正电的油滴,从M点运动到N点
B . 可能是带正电的油滴,从N点运动到M点
C . 可能是带负电的油滴,从M点运动到N点
D . 可能是带负电的油滴,从N点运动到M点
如图甲,两水平金属板间距为d,板间电场强度的变化规律如图乙所示。t=0时刻,质量为m的带电微粒以初速度v0沿中线射入两板间,
 时间内微粒匀速运动,T时刻微粒恰好经金属边缘飞出。微粒运动过程中未与金属板接触。重力加速度的大小为g。关于微粒在0~T时间内运动的描述,正确的是( )
时间内微粒匀速运动,T时刻微粒恰好经金属边缘飞出。微粒运动过程中未与金属板接触。重力加速度的大小为g。关于微粒在0~T时间内运动的描述,正确的是( )

A . 末速度大小为 B . B.末速度沿水平方向
C . C.重力势能减少了
B . B.末速度沿水平方向
C . C.重力势能减少了 D . D.克服电场力做功为mgd
D . D.克服电场力做功为mgd
 B . B.末速度沿水平方向
C . C.重力势能减少了
B . B.末速度沿水平方向
C . C.重力势能减少了 D . D.克服电场力做功为mgd
D . D.克服电场力做功为mgd
如图所示,两平行金属板水平放置,并接到电源上,一带电微粒p位于两板间处于静止状态,Ol、O2分别为两个金属板的中点,现将两金属板在极短的时间内都分别绕垂直于O1、O2的轴在纸面内逆时针旋转一个角θ(θ<90°),则下列说法中正确的是( )

A . 两板间的电压不变
B . 两板间的电压变小
C . 微粒P受到的电场力不变
D . 微粒将水平向左作直线运动
如图,A,B为平行板电容器,两板相距d,接在电压为U的电源上,在A板的中央有一小孔M(两板间电场可视为匀强电场).今有一质量为m的带电质点,自A板上方与A板相距也为d的O点由静止自由下落,穿过小孔M后到达距B板 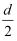 的N点时速度恰好为零.(重力加速度为g)求:
的N点时速度恰好为零.(重力加速度为g)求:
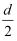 的N点时速度恰好为零.(重力加速度为g)求:
的N点时速度恰好为零.(重力加速度为g)求:
-
(1) 带电质点的电荷量,并指出其带电性质;
-
(2) 在保持与电源相连的情况下,A板往下移
 的距离.质点仍从O点由静止自由下落,求质点下落速度为零时距B板的距离.
的距离.质点仍从O点由静止自由下落,求质点下落速度为零时距B板的距离.
如图所示,水平放置的平行板电容器,两板间距为d=8cm,板长为L=25cm,接在直流电源上,有一带电液滴以υ0=0.5m/s的初速度从板间的正中央水平射入,恰好做匀速直线运动,当它运动到P处时迅速将下板向上提起  cm,液滴刚好从金属板末端飞出,求:
cm,液滴刚好从金属板末端飞出,求:
 cm,液滴刚好从金属板末端飞出,求:
cm,液滴刚好从金属板末端飞出,求:
-
(1) 将下板向上提起后,液滴的加速度大小;
-
(2) 液滴从射入电场开始计时,匀速运动到P点所用时间为多少?(g取10m/s2)
如图所示,表面粗糙的斜面固定于地面上,并处于方向垂直纸面向里的磁场和竖直向上的匀强电场中,磁感应强度大小为B,电场强度大小为E.一质量为m、带电量为﹣Q的小滑块从斜面顶端由静止下滑,在滑块下滑过程中,下列判断正确的是( )

A . 滑块受到的摩擦力不变
B . 若斜面足够长,滑块可能最终在斜面上匀速下滑
C . 若B足够大,滑块可能最终静止于斜面上
D . 滑块到达地面时的动能与B的大小有关
带等量异种电荷的金属板M、N平行正对水平放置,间距为d,M板中心有一小孔(小孔对电场的影响可忽略不计).一带电微粒从M板上方高d处的P点由静止开始下落,穿过M板的小孔后刚好到达N板处的Q点(但未触及N板)而返回.不计空气阻力,忽略金属板正对部分之外的电场.现将M板向上平移 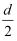 的距离,再让原带电微粒从P点由静止开始下落.则微粒的运动情况为( )
的距离,再让原带电微粒从P点由静止开始下落.则微粒的运动情况为( )

A . 落到N板上
B . 到达与N板相距d就返回
C . 到达与N板相距 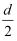 就返回
D . 仍刚好到达Q点而返回
就返回
D . 仍刚好到达Q点而返回
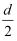 就返回
D . 仍刚好到达Q点而返回
就返回
D . 仍刚好到达Q点而返回
如图所示,竖直放置的两个平行金属板间有匀强电场,在两板之间等高处有两个质量相同的带电小球,P小球从紧靠左极板处由静止开始释放,Q小球从两板正中央由静止开始释放,两小球最后都能打在右极板上的同一点.则从开始释放到打到右极板的过程中( )

A . 它们的运动时间tP=tQ
B . 它们的电荷量之比qP:qQ=1:1
C . 它们的动能增加量之比△EkP:△EkQ=4:1
D . 它们的电势能减少量之比△EP:△EQ=4:1
如图所示,某空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,已知一离子在电场力和磁场力作用下,从静止开始沿曲线acb运动,到达b点时速度为零,c为运动的最低点.则( )

A . 离子必带负电
B . a、b两点位于同一高度
C . 离子在c点速度最大
D . 离子到达b点后将沿原曲线返回
场强为E的匀强电场和磁感强度为B的匀强磁场正交.如图质量为m的带电粒子在垂直于磁场方向的竖直平面内,做半径为R的匀速圆周运动,设重力加速度为g,则下列结论不正确的是( )

A . 粒子带负电,且q=  B . 粒子顺时针方向转动
C . 粒子速度大小v=
B . 粒子顺时针方向转动
C . 粒子速度大小v=  D . 粒子的机械能守恒
D . 粒子的机械能守恒
 B . 粒子顺时针方向转动
C . 粒子速度大小v=
B . 粒子顺时针方向转动
C . 粒子速度大小v=  D . 粒子的机械能守恒
D . 粒子的机械能守恒
如图所示,一电子束垂直于电场线与磁感线方向入射后偏向A极板,为了使电子束沿射入方向做直线运动,可采用的方法是( )

A . 将变阻器滑动头P向右滑动
B . 将变阻器滑动头P向左滑动
C . 将极板间距离适当减小
D . 将极板间距离适当增大
如图所示,两金属板间有水平方向(垂直纸面向里)的匀强磁场和竖直向下的匀强电场.一带正电、质量为m的小球垂直于电场和磁场方向从O点以速度v0飞入此区域,恰好能沿直线从P点飞出此区域.如果只将电场方向改为竖直向上,则小球做匀速圆周运动,加速度大小为a1 , 经时间t1从板间的右端a点飞出,a与P间的距离为y1;如果同时撤去电场和磁场,小球加速度大小为a2 , 经时间t2从板间的右端b点以速度v飞出,b与P间的距离为y2 . a、b两点在图中未标出,则一定有( )

A . v0<v
B . a1>a2
C . a1=a2
D . t1<t2
如图所示,半径R=0.8m的光滑绝缘导轨固定于竖直平面内,加上某一水平方向的匀强电场时,带正电的小球沿轨道内侧做圆周运动,它的电量q=1.00×10﹣7C.圆心O与A点的连线与竖直成一角度θ,在A点时小球对轨道的压力N=1.2N,此时小球的动能最大.若小球的最大动能比最小动能多0.32J,且小球能够到达轨道上的任意一点(不计空气阻力,g取10m/s2).则:

-
(1) 小球的最小动能是多少?
-
(2) 小球受到重力和电场力的合力是多少?
-
(3) 现小球在动能最小的位置突然撤去轨道,并保持其他量都不变,若小球在0.4s后的动能与它在A点时的动能相等,求小球的质量和电场强度.
如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,与两极板上边缘等高处有两个带负电小球A和B,它们均从两极板正中央由静止开始释放,两小球最终均打在极板上,(不考虑小球间的相互作用及对电场的影响)下列说法中正确的是( )

A . 两小球在两板间运动的轨迹都是一条抛物线
B . 两板间电压越大,小球在板间运动的时间越短
C . 它们的运动时间一定相同
D . 若两者的比荷相同,它们的运动轨迹可能相同
如图甲,两个绝缘的足够大的挡板M、N竖直放置,两板间存在一个竖直向上的匀强电场,另外有一个垂直纸面的匀强磁场,磁场的磁感应强度随时间变化的图象如图乙所示(以垂直纸面向外的方向为正,B0和T0为已知量).在t= 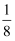 T0时刻,两个完全相同带正电的小球A、B以相同大小的初速度v0分别从紧贴M、N两板的位置水平射入电磁场中,在t=
T0时刻,两个完全相同带正电的小球A、B以相同大小的初速度v0分别从紧贴M、N两板的位置水平射入电磁场中,在t= 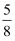 T0两球发生第一次碰撞,假设两个小球之间、小球与挡板之间的碰撞均为弹性碰撞,不计碰撞时间,且每次碰撞小球所带电荷量不变,已知小球的比荷为
T0两球发生第一次碰撞,假设两个小球之间、小球与挡板之间的碰撞均为弹性碰撞,不计碰撞时间,且每次碰撞小球所带电荷量不变,已知小球的比荷为  ,且小球所受电场力大小等于重力的大小,重力加速度为g,不考虑空气阻力及磁场变化产生的电场,则
,且小球所受电场力大小等于重力的大小,重力加速度为g,不考虑空气阻力及磁场变化产生的电场,则
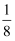 T0时刻,两个完全相同带正电的小球A、B以相同大小的初速度v0分别从紧贴M、N两板的位置水平射入电磁场中,在t=
T0时刻,两个完全相同带正电的小球A、B以相同大小的初速度v0分别从紧贴M、N两板的位置水平射入电磁场中,在t= 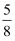 T0两球发生第一次碰撞,假设两个小球之间、小球与挡板之间的碰撞均为弹性碰撞,不计碰撞时间,且每次碰撞小球所带电荷量不变,已知小球的比荷为
T0两球发生第一次碰撞,假设两个小球之间、小球与挡板之间的碰撞均为弹性碰撞,不计碰撞时间,且每次碰撞小球所带电荷量不变,已知小球的比荷为  ,且小球所受电场力大小等于重力的大小,重力加速度为g,不考虑空气阻力及磁场变化产生的电场,则
,且小球所受电场力大小等于重力的大小,重力加速度为g,不考虑空气阻力及磁场变化产生的电场,则
-
(1) 求电场强度E的大小;
-
(2) 画出两个小球的运动轨迹并求出两板间距d的大小;
-
(3) 求出两个小球所有的碰撞时刻.
如图所示是对光电效应中产生的光电子进行比荷测定的原理图,两块平行金属板相距很近,板间距为d,放在真空中,其中N为锌板,受紫外线照射后将激发出沿不同方向的光电子,光电子打在M板上形成电流,引起微安表指针偏转,若调节变阻器R,逐渐增大两板间电压,可以使光电流逐渐减小到零,当电压表读数为U时,电流恰好为零。断开开关,在MN之间加一垂直纸面的磁场,逐渐增大磁感应强度,也能使光电流逐渐减小到零,此时的磁感应强度为B,那么光电子的比荷为。

如图所示,在xOy平面内,0<x<2L的区域内有一方向竖直向上的匀强电场,2L<x<3L的区域内有方向竖直向下的匀强电场,两电场强度大小相等。x>3L的区域内有一方向垂直于xOy平面向外的匀强磁场。某时刻,一带正电的粒子从坐标原点以沿x轴正方向的初速度 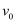 进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场。正、负粒子从电场进入磁场时速度方向与电场和碰场边界的夹角分别为60℃和30°,两粒子在磁场中分别运动半周后在某点相遇。已经两粒子的重力以及两粒子之间的相互作用都可忽略不计,两粒子带电量大小相等。求:
进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场。正、负粒子从电场进入磁场时速度方向与电场和碰场边界的夹角分别为60℃和30°,两粒子在磁场中分别运动半周后在某点相遇。已经两粒子的重力以及两粒子之间的相互作用都可忽略不计,两粒子带电量大小相等。求:
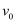 进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场。正、负粒子从电场进入磁场时速度方向与电场和碰场边界的夹角分别为60℃和30°,两粒子在磁场中分别运动半周后在某点相遇。已经两粒子的重力以及两粒子之间的相互作用都可忽略不计,两粒子带电量大小相等。求:
进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场。正、负粒子从电场进入磁场时速度方向与电场和碰场边界的夹角分别为60℃和30°,两粒子在磁场中分别运动半周后在某点相遇。已经两粒子的重力以及两粒子之间的相互作用都可忽略不计,两粒子带电量大小相等。求:
-
(1) 正、负粒子的质量之比ml: m2;
-
(2) 两粒子相遇的位置P点的坐标;
-
(3) 两粒子先后进入电场的时间差。
最近更新
- [化学——-选修5:有机化学基础](15分)有机
- 平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方
- A、B、C为短周期元素,在周期表中如右图所示
- — John, where are the cookies? Don't tell me you ate them
- 下面标点符号使用正确的一项是( ) A. 请闭
- 石板路上踏过的青春 骆非翔(14分) ①他作
- X、Y、Z是三种不同的金属,将X、Y分别放入稀
- 漂浮在水面上的皮球,用手将其慢慢压入水
- 使吸入的气体变得清洁的结构有( ) ①声带
- 下列物质与其对应的用途不相符的是 A. 稀有
- 我国曾经发射了一颗“北斗一号”导航定位卫
- 某稀溶液中含有等物质的量的ZnSO4、Fe2(SO4)3、H
- 中国茶道 茶道不同于一般的饮茶。在中国饮
- There______a pen and six books on your desk. A. be �
- 某工厂排放的酸性废水中含有较多的Cu2+,对
- 《大国崛起》解说词中说:“三百年前,人类
- 2014年前三季度,我国境内投资者共对全球152
- . US President Barack Obama made his first visit to China ea
- 不同环境中的被子植物有其特定的适应方式。
- 具有鲜明中国特色的选官方式是:



