终边相同的角 知识点题库
根据角度制和弧度制的转化,已知条件:α=1690°,
-
(1) 把α表示成2kπ+β的形式(k∈Z,β∈[0,2π));
-
(2) 求θ,使θ与α的终边相同,且θ∈(﹣4π,﹣2π).
下列各角与角420°终边相同的是( )
A . 30°
B . 60°
C . 120°
D . 300°
若角α+ 的顶点为坐标原点,始边与x轴的非负半轴重合,终边在直线y=
的顶点为坐标原点,始边与x轴的非负半轴重合,终边在直线y= x上,则tanα的值为
x上,则tanα的值为
 的顶点为坐标原点,始边与x轴的非负半轴重合,终边在直线y=
的顶点为坐标原点,始边与x轴的非负半轴重合,终边在直线y= x上,则tanα的值为
x上,则tanα的值为
与2016°终边相同的最小正角是
有小于180°的正角,这个角的9倍角的终边与这个角的终边重合,求这个角的度数.
写出与  终边相同的角的集合S,并把S中适合不等式﹣2π≤β<4π的元素β写出来.
终边相同的角的集合S,并把S中适合不等式﹣2π≤β<4π的元素β写出来.
 终边相同的角的集合S,并把S中适合不等式﹣2π≤β<4π的元素β写出来.
终边相同的角的集合S,并把S中适合不等式﹣2π≤β<4π的元素β写出来.
与﹣527°角终边相同的角的集合是( )
A . {α|α=k⋅360°+527°,k∈Z}
B . { α|α=k⋅360°+157°,k∈Z }
C . {α|α=k⋅360°+193°,k∈Z }
D . { α|α=k⋅360°﹣193°,k∈Z }
与角﹣  终边相同的角是( )
终边相同的角是( )
 终边相同的角是( )
终边相同的角是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下面表述不正确的是( )
A . 终边在x轴上角的集合是{α|α=kπ,k∈Z}
B . 终边在y轴上角的集合是  C . 终边在坐标轴上的角的集合是
C . 终边在坐标轴上的角的集合是  D . 终边在直线y=﹣x上角的集合是
D . 终边在直线y=﹣x上角的集合是 
 C . 终边在坐标轴上的角的集合是
C . 终边在坐标轴上的角的集合是  D . 终边在直线y=﹣x上角的集合是
D . 终边在直线y=﹣x上角的集合是 
若α=1690°,θ与α的终边相同,且0°<θ<360°,则θ=( )
A . 300°
B . 250°
C . 200°
D . 150°
设角α是第三象限角,且  ,则角
,则角  是第象限角.
是第象限角.
 ,则角
,则角  是第象限角.
是第象限角.
将﹣1485°化为2kπ+α(0≤α<2π,k∈Z)的形式是.
角的终边在第一象限和第三象限的平分线上的角的集合为.
与α=  +2kπ(k∈Z)终边相同的角是( )
+2kπ(k∈Z)终边相同的角是( )
 +2kπ(k∈Z)终边相同的角是( )
+2kπ(k∈Z)终边相同的角是( )
A . 345°
B . 375°
C . ﹣  π
D .
π
D .  π
π
 π
D .
π
D .  π
π
在  中与
中与  终边相同的角有( )
终边相同的角有( )
 中与
中与  终边相同的角有( )
终边相同的角有( )
A . 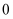 个
B .
个
B .  个
C .
个
C .  个
D .
个
D .  个
个
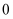 个
B .
个
B .  个
C .
个
C .  个
D .
个
D .  个
个
与-60°的终边相相同的角是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列说法正确的是( )
A . 与角  终边相同的角
终边相同的角  的集合可以表示为
的集合可以表示为  B . 若
B . 若  为第一象限角,则
为第一象限角,则  为第一或第三象限角
C . 函数
为第一或第三象限角
C . 函数  是偶函数,则
是偶函数,则  的一个可能值为
的一个可能值为  D . “
D . “  ”是函数
”是函数  的一条对称轴
的一条对称轴
 终边相同的角
终边相同的角  的集合可以表示为
的集合可以表示为  B . 若
B . 若  为第一象限角,则
为第一象限角,则  为第一或第三象限角
C . 函数
为第一或第三象限角
C . 函数  是偶函数,则
是偶函数,则  的一个可能值为
的一个可能值为  D . “
D . “  ”是函数
”是函数  的一条对称轴
的一条对称轴
2021º是第象限的角.
在 ,
,  ,
,  ,
,  中,与
中,与 终边相同的是( )
终边相同的是( )
 ,
,  ,
,  ,
,  中,与
中,与 终边相同的是( )
终边相同的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知 是第一象限角,且角
是第一象限角,且角 的终边关于y轴对称,则
的终边关于y轴对称,则 ( )
( )
 是第一象限角,且角
是第一象限角,且角 的终边关于y轴对称,则
的终边关于y轴对称,则 ( )
( )
A .  B .
B .  C .
C . 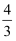 D .
D . 
 B .
B .  C .
C . 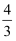 D .
D . 
最近更新
- .若 。
- 以下四个图象能正确反映对应变化关系的是 ① ②
- 成语“万事俱备,只欠东风”是根据《三国演义》____________(战役)中”周瑜定计火攻曹操”的故事演化而来的。请再
- 已知f(x)=asinx + btanx+2,且满足f()=7,求f()的值.
- 如图所示,同一物体沿相同水平地面被滑轮或滑轮组匀速拉动,拉力分别为F甲、F乙、 F丙,不计滑轮与轴及轻绳间的摩擦
- 魏源在《海国图志·大西洋英吉利国》中介绍“设有用兵和战之事,虽国王裁夺,亦必由巴厘满议允。国王行事有失,将承行之人交巴厘
- 温度与我们的生活息息相关,你仔细观察过温度计吗?如图12是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是
- 选择填空—Can you believe that Ning Zetao, a 21-year-old boy, won
- 平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要
- 为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3
- 自然界中种类最多的一类动物是( ) A.哺乳动物 B.昆虫 C.鱼类 D.爬行动物
- 填入下列句中横线处的语句,顺序最恰当的一项是 ( ) 今儿晚上,这感情又来袭击我了,仿佛二十多年来我并没
- 近年,福建某市投巨资建设基层公共文化服务设施,公共博物馆、美术馆、图书馆、文化馆、乡镇综合文化站等全部实现免费开放,假若
- 下列类比关系正确的是 A.钠与氧气在不同条件下反应会生成两种不同的氧化物,则Li与氧气反应也能生成Li2O或Li2O2
- 26、豌豆子叶的黄色(Y)、圆粒种子(R)均为显性,两亲本杂交的F1的表现型如图。让F1中黄色圆粒豌豆与绿色皱粒豌豆杂交
- 阅读下面的文言文,翻译文中画线的句子: 孟子去齐,充虞路问曰:“夫子若有不豫色然。前日虞闻诸夫子曰:‘君子不怨天,不尤人
- 国家预防腐败局被列入国务院直属机构序列,其与纪检系统、监察部门、检察院反贪局的工作是相辅相成的。从我国的行政监督体系看,
- 某同学将甲、乙两种植物种植在成分相同的土壤中,分成A、B、C、D、四组(如图所示),其中B与C遮光,降低光照30%,请回
- 中国2010年上海世界博览会,于 2010年5月1日~10月31日举办。据此回答下列小题 上海世博会的门票分为平日普通票
- 把下列各数填在相应的大括号里(将各数用逗号分开): ﹣4,0.62,,18,0,﹣8.91,+100 正数:{…} 负数



