统计表 知识点题库
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:

-
(1) 训练后篮球定时定点投篮人均进球数为 个;
-
(2) 选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
-
(3) 根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
年级 | 七年级 | 八年级 | 九年级 |
合格人数 | 270 | 262 | 254 |
北京市统计局发布了2014年人口抽样调查报告,首次增加了环线人口分布数据.调查数据显示,北京市超过一半的常住人口都住在了远离城区的五环以外.事实上,北京市的中心城区人口从上世纪80年代起就持续下降,越来越多的人向郊区迁移.
根据2014年人口抽样调查结果发现,本市三环至六环间,聚集了1226.9万人的常住人口,占全市的57.1%;四环至六环间聚集了941万人的常住人口,占全市的43.8%;五环以外有1098万人的常住人口,占全市的51.1%.
在进行人口分布研究时,北京通常被划分为四个区域,城市功能拓展区包括:朝阳、海淀、丰台、石景山四个区; 城市发展新区包括:通州、顺义、大兴、昌平、房山五个区和亦庄开发区; 首都功能核心区包括:东城区和西城区; 生态涵养发展区包括:门头沟、平谷、怀柔、密云、延庆五个区县.
从常住人口分布上看:城市功能拓展区常住人口最多,占全市总量的49%;城市发展新区常住人口约为684万人;首都功能核心区常住人口约为221万人;生态涵养发展区常住人口约为191万人.
从常住外来人口分布上看:城市功能拓展区常住外来人口最多,约为436万人;城市发展新区常住外来人口约为297万人;首都功能核心区常住外来人口约为54万人;生态涵养发展区常住外来人口约为32万人.
根据以上材料回答下列问题:
(1)估算2014年北京市常住人口约为多少万人.
(2)选择统计表或统计图,将2014年北京市按四个区域的常住人口和常住外来人口分布情况表示出来.
①完成表中的空格信息;
②5人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
姓名 | 王芳 | 刘兵 | 张昕 | 李聪 | 江文 |
成绩 | 89 | 84 | |||
与全班平 均分之差 | ﹣1 | +2 | 0 | ﹣2 |

学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题:
-
(1) x=,a=,b=;
-
(2) 补全上面的条形统计图;
-
(3) 若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.

已知全班同学此题的平均得分为4分,结合表格解决下列问题:
-
(1) 完成表格,并求该班学生总数;
-
(2) 根据表中提供的数据,补全条形统计图;并判断下列说法中正确的有.(填序号即可)
①该班此题得分的众数是6;
②“随机抽取该班一份试卷,此题得1分”是不可能事件;
③该班学生此题得分的中位数是4;
④若将“该班同学本道题的得分情况”绘制成扇形统计图,求“此题得0分”的人数所对应的圆心角的度数为36°;
-
(3) 若本年级学生共有540人,请你估计整个年级中此题得满分的学生人数.

-
(1) 补充完整乙组数据的折线统计图。
-
(2) ①甲,乙两组数据的平均数分别为了
 ,
,  ,写出
,写出  与
与  之间的等量关系.
之间的等量关系.
②甲,乙两组数据的方差分别为S甲2 , S乙2 , 比较S甲2与S乙2的大小,并说明理由.
各类别的得分表
|
得分 |
类别 |
|
| |
| | |
| | |
| | |
已知两个班一共有 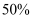 的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为
的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为  分.请解决如下问题:
分.请解决如下问题:

-
(1) 九(2)班学生得分的中位数是 ;
-
(2) 九(1)班学生中这道试题作答情况属于
 类和
类和  类的人数各是多少?
类的人数各是多少?
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
根据统计数据制作了如下统计表:
|
时间x |
x≤30 |
30<x≤60 |
60<x≤90 |
90<x≤120 |
|
男生 |
2 |
8 |
8 |
2 |
|
女生 |
1 |
4 |
a |
3 |
两组数据的极差、平均数、中位数、众数如下表所示:
|
极差 |
平均数 |
中位数 |
众数 |
|
|
男生 |
100 |
65.75 |
b |
c |
|
女生 |
90 |
75.5 |
75 |
75 |
-
(1) 请将上面两个表格补充完整:
a=,b=,c=;
-
(2) 请根据抽样调查的数据估计初三年级周末每天运动时间在100分钟以上的同学大约有多少人?
-
(3) 李老师看了表格数据后认为初三年级的女生周末体锻坚持得比男生好,请你结合统计数据,写出支持李老师观点的理由.
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在C组中的数据是:94,90,94
七八年级抽取的学生竞赛成绩统计表:
|
年级 |
平均数 |
中位数 |
众数 |
方差 |
|
七年级 |
92 |
93 |
c |
52 |
|
八年级 |
92 |
b |
100 |
50.4 |

根据以上信息,解答下列问题:
-
(1) 直接写出上述图表中a、b、c的值:a=、b=、c=.
-
(2) 由以上数据,你认为该校七、八年级中哪个年级学生掌握“新冠疫情”防控知识较好?请说明理由(一条理由即可);
-
(3) 该校七、八年级参加此次竞赛活动的人数分别为1200人和1300人,估计在本次竞赛活动中七、八年级成绩优秀(x≥90)的学生人数共有多少?
调查结果统计表
|
学科 |
语文 |
英语 |
数学 |
物理 |
化学 |
|
人数(人) |
12 |
30 |
|
54 |
9 |

请根据以上信息,解答下列问题:
-
(1) 本次共调查了名学生,
 ,
, 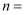 _;
_;
-
(2) 扇形统计图中,数学所在扇形圆心角的度数为多少?
-
(3) 该校九年级共有
 名学生,根据调查结果,请你估计该校最喜爱英语网课的学生人数.
名学生,根据调查结果,请你估计该校最喜爱英语网课的学生人数.
七年级学生最喜欢的球类运动项目人数统计表
|
项目 |
排球 |
篮球 |
足球 |
乒乓球 |
其它 |
|
人数(人) |
7 |
8 |
14 |
6 |
八年级学生最喜欢的球类运动项目人数统计图

九年级学生最喜欢的球类运动项目人数统计图

请根据统计表(图)解答下列问题:
-
(1) 本次调查共抽取了多少名学生?
-
(2) 补全统计表和统计图,并求出“最喜欢乒乓球”的学生占抽样总人数的百分比.
甲班15名学员测试成绩(满分100分)统计如下:
87,84,88,76,93,87,73,98,86,87,79,85,84,85,98.
乙班15名学员测试成绩(满分100分)统计如下:
77,88,92,85,76,90,76,91,88,81,85,88,98,86,89.

-
(1) 按如下分数段整理两班测试成绩
班级
70.5~75.5
75.5~80.5
80.5~85.5
85.5~90.5
90.5~95.5
95.5~100.5
甲
1
2
a
5
1
2
乙
0
3
3
6
2
1
表中
 ;
; -
(2) 补全甲班15名学员测试成绩的频数分布直方图;

-
(3) 两班测试成绩的平均数、众数、中位数、方差如表所示:
班级
平均数
众数
中位数
方差
甲
86

86
44.8
乙
86
88
y
36.7
表中
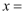 ,
,  .
. -
(4) 以上两个班级学员掌握党史相关知识的整体水平较好的是班;
-
(5) 本次测试两班的最高分都是98分,其中甲班2人,乙班1人.现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛,利用树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率.
|
劳动时间(时) |
人数 |
占整体的百分比 |
|
0.5 |
12 |
12% |
|
1 |
30 |
30% |
|
1.5 |
x |
40% |
|
2 |
18 |
y |
|
合计 |
m |
100% |

-
(1) 统计表中的x=,y=;
-
(2) 被调查同学劳动时间的中位数是 时;
-
(3) 请将条形统计图补充完整;
-
(4) 求所有被调查同学的平均劳动时间.
-
(5) 若该校有1500名学生,试估计双休日在各自社区参加2小时义务劳动的学生有多少?

-
(1) 90分及以上为A级,75~89分为B级,60~74分为C级,60分以下为D级.请把下面表格补充完整,并将图中的条形图补充完整;
等级
A
B
C
D
人数
▲
▲
8
▲
-
(2) 该校九年级共有1000名学生,如果75分以上为良好,请估计九年级有多少学生的成绩为良好?
-
(3) 请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
| 年级 |
参加英语听力训练人数 |
||||
| 周一 |
周二 |
周三 |
周四 |
周五 |
|
| 七年级 |
15 |
20 |
|
30 |
30 |
| 八年级 |
20 |
24 |
26 |
30 |
30 |
| 合计 |
35 |
44 |
51 |
60 |
60 |

-
(1) 填空:
 ;
;
-
(2) 根据上述统计图表完成下表中的相关统计量:
年级
平均训练时间的中位数
参加英语听力训练人数的方差
七年级
24
34
八年级
14.4
-
(3) 请你利用上述统计图表,对七、八年级英语听力训练情况写出两条合理的评价;
-
(4) 请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.
竞赛成绩统计表(成绩满分100分)
组别 | 分数 | 人数 |
A组 | 75<x≤80 | 4 |
B组 | 80<x≤85 | b |
C组 | 85<x≤90 | 10 |
D组 | 90<x≤95 | d |
E组 | 95<x≤100 | 14 |
合计 | ||

根据统计图表提供的信息,解答下列问题:
-
(1) 本次共调查了名学生;b=;
-
(2) 求C组所在扇形的圆心角的度数;
-
(3) 该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?
a.第一次体育测试成绩统计表:
分组/分 | 人数 |
| 1 |
| 1 |
| 9 |
|
|
| 3 |
b.第二次体育测试成绩统计图:

c.两次成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
第一次成绩 | 19.7 |
| 19 |
第二次成绩 | 25 | 26.5 | 28 |
d.第一次体育测试成绩在 这一组的数据是:15,16,17,17,18,18,19,19,19.
这一组的数据是:15,16,17,17,18,18,19,19,19.
e.第二次体育测试成绩在 这一组的数据是:17,19.
这一组的数据是:17,19.
请根据以上信息,回答下列问题:
-
(1) m=,n=;
-
(2) 第二次体育测试成绩为
 得分组所对应的圆心角度数是;第二次体育测试成绩的及格率(大于或等于18分为及格)为;
得分组所对应的圆心角度数是;第二次体育测试成绩的及格率(大于或等于18分为及格)为;
-
(3) 下列推断合理的是.
①第二次测试成绩的平均分高于第一次的平均分,所以大多数学生通过此种方法锻炼一段时间后成绩都提升了.
②被抽测的学生小明的第二次测试成绩是24分,他觉得年级里大概有240人的测试成绩比他高.
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
乙班15名学生测试成绩中 的成绩如下:91,92,94,90,93
的成绩如下:91,92,94,90,93
【整理数据】
班级 |
|
|
|
|
|
甲 | 1 | 1 | 3 |
| 6 |
乙 | 1 | 2 | 3 | 5 | 4 |
【分析数据】
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 92 |
| 93 | 41.7 |
乙 | 90 | 87 |
| 50.2 |
【应用数据】
-
(1) 根据以上信息,可以求出:
 ,
,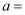 分,
分,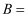 分;
分;
-
(2) 根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?并至少从两个方面说明理由.
七年级10名学生的竞赛成绩是80,86,99,96,90,99,100,82,89,99;
八年级10名学生的竞赛成绩在C组中的数据是94,94,90.
七,八年级抽取的学生竞赛成绩统计表
|
七年级 |
八年级 |
|
|
平均数 |
92 |
92 |
|
中位数 |
93 |
b |
|
众数 |
a |
100 |
|
方差 |
52 |
50.4 |

根据以上信息,解答下列问题:
-
(1) 填空:a=,b=,c=.
-
(2) 根据以上数据,你认为该校七、八年级中哪个年级的学生掌握防溺水安全知识的情况更好?请说明理由(一条即可).
-
(3) 已知该校七、八年级共960人参加了此次竞赛,估计参加此次竞赛成绩为优秀(x≥95)的学生人数.
- 如图表示两种气体发生化学反应的微观示意图
- 旅游公司为3个旅游团提供甲、乙、丙、丁4条
- (7分)下图表示动物、植物细胞二合一亚显
- 白毛羊与白毛羊通过有性生殖产生的后代中出
- 某商场今年销售计算机5000台.如果平均每年
- 用落体法验证机械能守恒定律的实验中 (1)
- 原子最外层失去或得到电子后,一定不发生变
- 清晨入古寺, 。(常
- 历史遗迹是了解历史的重要学习途径。图2遗
- 在“用显微镜观察洋葱表皮细胞”的实验中,
- —I'm sorry to keep you waiting. I'll make short work of th
- 已知二次函数的最大值为0,则( )A、 �
- 如图所示的①②③表示人体细胞间信息传递的
- 人体形成听觉的部位在( )A. 听觉感受器 B
- 下列各组词语中,有错别字的一组是
- 与其他介于英美两制之间的国家的政体相比,
- 求值:____.
- —you come to my party on Sunday? —Sorry,I’m not ava
- Looking ahead to 2010, it appears financially impossible to
- 依次填入下面一段文字横线处的语句,衔接最
 :没有作答
:没有作答


 :得到两个正确答案,解答完全正确
:得到两个正确答案,解答完全正确












