2018жІіеҢ—й«ҳдёүдёҠеӯҰжңҹй«ҳдёӯж•°еӯҰжңҹдёӯиҖғиҜ•
| 1. | иҜҰз»ҶдҝЎжҒҜ |
|
.и®ҫ AпјҺпјҚ1В В В В В В В В В В В В В В В В BпјҺ1В В В В В В В В В В В В CпјҺпјҚ2DпјҺ2
|
|
| 2. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫйӣҶеҗҲ AпјҺ3В В В В В В В В В В В В В В В В В В BпјҺ4В В В В В В В В В В В В CпјҺ5В В В В В В В В В В В В В DпјҺ6
|
|
| 3. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘеҗ‘йҮҸ AпјҺе……еҲҶдёҚеҝ…иҰҒжқЎд»¶В В В В В BпјҺеҝ…иҰҒдёҚе……еҲҶжқЎд»¶В В В В В В CпјҺе……иҰҒжқЎд»¶В В В В В В В DпјҺж—ўдёҚе……еҲҶд№ҹдёҚеҝ…иҰҒжқЎд»¶
|
|
| 4. | иҜҰз»ҶдҝЎжҒҜ |
|
дёӯеӣҪеҸӨд»Јж•°еӯҰеҗҚи‘—гҖҠд№қз« з®—жңҜгҖӢдёӯжңүиҝҷж ·дёҖдёӘй—®йўҳ:д»ҠжңүзүӣгҖҒ马гҖҒзҫҠйЈҹдәәиӢ—пјҢиӢ—дё»иҙЈд№ӢзІҹдә”ж–—пјҢзҫҠдё»жӣ°:вҖңжҲ‘зҫҠйЈҹеҚҠ马.вҖқ马主жӣ°:вҖңжҲ‘马йЈҹеҚҠзүӣ.вҖқд»Ҡж¬ІиЎ°еҒҝд№ӢпјҢй—®еҗ„еҮәеҮ дҪ•пјҹжӯӨй—®йўҳзҡ„иҜ‘ж–ҮжҳҜ:д»ҠжңүзүӣгҖҒ马гҖҒзҫҠеҗғдәҶеҲ«дәәзҡ„зҰҫиӢ—пјҢзҰҫиӢ—дё»дәәиҰҒжұӮиө”еҒҝ5ж–—зІҹ.зҫҠдё»дәәиҜҙ:вҖңжҲ‘зҫҠжүҖеҗғзҡ„зҰҫиӢ—еҸӘжңү马зҡ„дёҖеҚҠ.вҖқ马主дәәиҜҙ:вҖңжҲ‘马жүҖеҗғзҡ„зҰҫиӢ—еҸӘжңүзүӣзҡ„дёҖеҚҠ.вҖқжү“з®—жҢүжӯӨжҜ”дҫӢеҒҝиҝҳпјҢ他们еҗ„еә”еҒҝиҝҳеӨҡе°‘пјҹе·ІзҹҘзүӣгҖҒ马гҖҒзҫҠзҡ„дё»дәәеҗ„еә”еҒҝиҝҳ AпјҺ BпјҺ C. DпјҺ
|
|
| 5. | иҜҰз»ҶдҝЎжҒҜ |
|
иӢҘеҮҪж•° AпјҺ
|
|
| 6. | иҜҰз»ҶдҝЎжҒҜ |
|
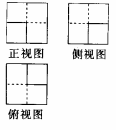
жҹҗеҮ дҪ•зҡ„дёүи§ҶеӣҫеҰӮеӣҫжүҖзӨәпјҢе…¶дёӯжҜҸдёӘи§Ҷеӣҫдёӯзҡ„еӣӣдёӘе°ҸжӯЈж–№еҪўзҡ„иҫ№й•ҝйғҪзӣёзӯүпјҢиӢҘиҜҘеҮ дҪ•дҪ“зҡ„дҪ“з§Ҝдёә
AпјҺ36В В В В В В В В В В В В В В В В В BпјҺ42В В В В В В В В В В В C. 48DпјҺ64
|
|
| 7. | иҜҰз»ҶдҝЎжҒҜ |
|
е®ҡд№үеңЁ AпјҺ
|
|
| 8. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫеҸҳйҮҸ AпјҺ[2пјҢ6]В В В В В В В В В В В В В BпјҺпјҲпјҚвҲһпјҢ10]В В В В В В C.[2пјҢ10]В В В В В В DпјҺпјҲпјҚвҲһпјҢ6]
|
|
| 9. | иҜҰз»ҶдҝЎжҒҜ |
|
еңЁеӣӣжЈұй”Ҙ AпјҺ
|
|
| 10. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫ AпјҺ C.
|
|
| 11. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫ AпјҺ
|
|
| 12. | иҜҰз»ҶдҝЎжҒҜ |
|
еҪ“ AпјҺ
|
|
| 13. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫеҗ‘йҮҸ
|
|
| 14. | иҜҰз»ҶдҝЎжҒҜ |
|
еҮҪж•°
|
|
| 15. | иҜҰз»ҶдҝЎжҒҜ |
|
.иӢҘеҮҪж•°
|
|
| 16. | иҜҰз»ҶдҝЎжҒҜ |
|
еҰӮеӣҫпјҢеңЁеӣӣжЈұй”Ҙ
|
|
| 17. | иҜҰз»ҶдҝЎжҒҜ |
|
еңЁ пјҲ1пјүжұӮ пјҲ2пјүжұӮ
|
|
| 18. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫ пјҲ1пјүжұӮ пјҲ2пјүи®°
|
|
| 19. | иҜҰз»ҶдҝЎжҒҜ |
|
В е·ІзҹҘеҗ‘йҮҸ пјҲ1пјүиӢҘ пјҲ2пјүжұӮ пјҲ3пјүе°Ҷ
|
|
| 20. | иҜҰз»ҶдҝЎжҒҜ |
|
еҰӮеӣҫ,еңЁдёүжЈұй”Ҙ пјҲ1пјүиӢҘ пјҲ2пјүжұӮдәҢйқўи§’
|
|
| 21. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘеҮҪж•° пјҲ1пјүжұӮжӣІзәҝ пјҲ2пјүиӢҘеҮҪж•°
|
|
| 22. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘеҮҪж•° пјҲ1пјүеҪ“ пјҲ2пјүи®ҫ
|
|
- еҫ·е·һеёӮ2019е№ҙй«ҳдёҖж•°еӯҰдёҠеҚҠжңҹжңҹжң«иҖғиҜ•иҜ•еҚ·еёҰи§ЈжһҗеҸҠзӯ”жЎҲ
- 2019еұҠй«ҳдёүдёҠеҶҢжңҹжң«иҖғиҜ•ж•°еӯҰйўҳе…Қиҙ№иҜ•еҚ·пјҲжұҹиҘҝзңҒдёҙе·қеёӮ第дёҖдёӯеӯҰпјү
- 2018-2019е№ҙй«ҳдәҢдёӢжңҹжңҹдёӯиҒ”иҖғж•°еӯҰиҜ•еҚ·е®Ңж•ҙзүҲпјҲжөҷжұҹзңҒжқӯе·һең°еҢә(еҗ«е‘Ёиҫ№)йҮҚзӮ№дёӯеӯҰпјү
- е®үеҫҪзңҒж»Ғе·һеёӮе®ҡиҝңеҺҝ2020-2021е№ҙй«ҳдёүдёҠеҶҢ第дәҢж¬ЎиҒ”иҖғж•°еӯҰ(зҗҶ)йўҳеёҰзӯ”жЎҲе’Ңи§Јжһҗ
- жөҷжұҹй«ҳдёүж•°еӯҰжңҲиҖғжөӢйӘҢпјҲ2020е№ҙдёӢеҚҠе№ҙпјүзҪ‘з»ңиҖғиҜ•иҜ•еҚ·
- дёӯеұұеёӮй«ҳдәҢж•°еӯҰдёӢеҶҢжңҹжң«иҖғиҜ•иҜ•еҚ·е®Ңж•ҙзүҲ
- 4.1+жҢҮж•°+еӯҰжЎҲ-иӢҸж•ҷзүҲй«ҳдёӯж•°еӯҰеҝ…дҝ®з¬¬дёҖеҶҢ
- й«ҳдёүж•°еӯҰдёҠеӯҰжңҹй«ҳиҖғжЁЎжӢҹеңЁзәҝеҒҡйўҳпјҲ2017е№ҙеӣӣе·қпјү
- дёӢеҲ—еҸҘеӯҗдёӯжІЎжңүиҜӯз—…зҡ„дёҖеҸҘжҳҜВ В В В В В В В В
- дёӢеҲ—е…ідәҺиғ¶дҪ“зҡ„еҸҷиҝ°дёҚжӯЈзЎ®зҡ„жҳҜ AпјҺиғ¶дҪ“еҢәеҲ«
- дёӢеҲ—еҮ з§ҚиҶңдёӯпјҢиғҪйҖҡиҝҮжҹҗдәӣеӨ§еҲҶеӯҗзү©иҙЁзҡ„жҳҜ В
- еңЁеҸҚеә”пјҡ11P+15CuSO4+24H2O=5Cu3P+6H3PO4+15H2SO4 дёӯ15molC
- жһҒеқҗж Үж–№зЁӢsinОё=(ПҒвҲҲR)иЎЁзӨәзҡ„жӣІзәҝжҳҜ( )оҖғA.дёӨ
- В вҖңйҡӢе”җж—¶жңҹпјҢдёӯеӣҪжӢҘжңүе…Ҳиҝӣзҡ„ж”ҝжІ»дҪ“еҲ¶вҖқпјҢ
- 科еӯҰеҸ‘еұ•и§Ӯзҡ„第дёҖиҰҒд№үжҳҜ A.еҸ‘еұ•В В В В В В В В В
- еҷ¬иҸҢдҪ“дҫөжҹ“з»ҶиҸҢзҡ„е®һйӘҢжүҖиғҪиҜҒе®һзҡ„DNAжҳҜйҒ—дј зү©
- йҳ…иҜ»зҹӯж–ҮпјҢж №жҚ®зҹӯж–ҮеҶ…е®№еӣһзӯ”дёӢеҲ—й—®йўҳжҲ–зҝ»иҜ‘
- жңҚйҘ°е’Ңд№ дҝ—зҡ„жөҒиЎҢдёҚд»…еҸҚжҳ ж—¶д»ЈжҖқжҪ®пјҢжңүж—¶д№ҹ
- дёҖе®ҡжқЎд»¶дёӢпјҢCH3COONaжә¶ж¶ІеӯҳеңЁж°ҙи§Је№іиЎЎпјҡCH3COO
- 20дё–зәӘе…«д№қеҚҒе№ҙд»ЈпјҢжҲ‘еӣҪеҗҢиӢҸиҒ”гҖҒи’ҷеҸӨгҖҒи¶ҠеҚ—
- з®Җиҝ°еңҹең°гҖҒи®ҫеӨҮгҖҒеҺҹжқҗж–ҷзӯүз”ҹдә§иҰҒзҙ еңЁе•Ҷе“Ғз”ҹ
- дёӢеҲ—еҜ№е®һйӘҢзҺ°иұЎзҡ„и§ӮеҜҹжҲ–и®°еҪ•дёӯжӯЈзЎ®зҡ„жҳҜ AпјҺ
- дёӢеҲ—иҪ¬еҢ–еёёйҖҡиҝҮеҸ–д»ЈеҸҚеә”е®һзҺ°зҡ„жҳҜ( ) AпјҺВ В В
- The most satisfying life is a life В В В В you know the thin
- жҹҗдәәеңЁжҢҒз»ӯеҮ еӨ©е’іе—ҪеҗҺеҸ‘зғӯпјҢз»ҸиҜҠж–ӯжҳҜз»ҶиҸҢж„ҹ
- е·ІзҹҘпјҡе…ідәҺзҡ„ж–№зЁӢпјҲ1пјүжұӮиҜҒпјҡж–№зЁӢжңүдёӨдёӘдёҚ
- 2010е№ҙ3жңҲпјҢдёӯеӨ®зәӘ委гҖҒдёӯеӨ®е®Јдј йғЁгҖҒзӣ‘еҜҹйғЁгҖҒ
- . The government has taken some measures to solve the shorta