七年级(初一)：语文　 数学　 英语　 生物　 历史　 道法　 地理　

七年级(初一)试题

小米同学对蜗牛对外界刺激做出反应的情况做了以下几种猜测，其中不可能的是（）

A . 用牙签轻触蜗牛，蜗牛会做出反应 B . 对着蜗牛大喊，蜗牛会做出反应 C . 把酒精擦在蜗牛要经过的桌子前面，蜗牛会做出反应 D . 用强光照射，蜗牛会做出反应

实验探究

某生物兴趣小组成员看到电视广告中某洗手液厂商标榜其洗手液有强效的“抗菌”能力。他们对此产生了疑问，于是设计并做了下列实验：

（1）实验方案如下：
①将配制好的培养基分别装入9个培养皿中，进行高温灭菌后随机分为三组，每组3个，分别编号A、B、C组；

②在教室中打开A、B两组的培养皿，暴露在空气中20分钟，C组不做任何处理；设置C组的实验目的是。

③在A组培养皿中加入，B组培养皿中加入2ml无菌水，C组不作处理；

④将9个培养皿盖好，分类放入恒温箱中，在30℃条件下培养3天，每天观察两次并记录。（注意不要打开培养皿）
（2）预测实验结果与结论：
①若统计记录结果是：A组菌落平均数较少，B组菌落平均数较多，C组无菌落或菌落平均数较少，则说明。

②若统计记录结果是：A组、B组菌落平均数较多，C组无菌落或菌落平均数较少，则说明。
（3）实验设计A、B、C三组时，每组设置3个培养皿，取菌落的平均数，而不是只设置1个培养皿，他们的设计目的是。

他主张：“夫仁政，必自经界(土地的分界)始。”“他”是( )

A . 庄子 B . 孟子 C . 荀子 D . 墨子

某市计划对道路进行维护．已知甲工程队每天维护道路的长度比乙工程队每天维护道路的长度多50%，甲工程队单独维护30千米道路的时间比乙工程队单独维护24千米道路的时间少用1天．

（1）求甲、乙两工程队每天维护道路的长度是多少千米？
（2）若某市计划对200千米的道路进行维护，每天需付给甲工程队的费用为25万元，每天需付给乙工程队的费用为15万元，考虑到要不超过26天完成整个工程，因工程的需要，两队均需参与，该市安排乙工程队先单独完成一部分，剩下的部分两个工程队再合作完成．问乙工程队先单独做多少天，该市需付的整个工程费用最低？整个工程费用最低是多少万元？

单项式 $\text{[math]}$ 的系数是，次数是.

中国与巴西的合作称为“南南合作”，“南南合作”的意思是（）

A . 中国是南亚国家，巴西是南美洲国家 B . 这里的“南”代指发展中国家，“南南合作”指的是发展中国家之间的合作 C . 中国和巴西都是南半球国家 D . 中国是南亚国家，巴西是南半球国家

下列细胞结构中，杜鹃鸟和杜鹃花细胞共有的是（）

①细胞壁

②细胞膜

③线粒体

④叶绿体

⑤细胞核

A . ②④⑤ B . ①④ C . ②③⑤ D . ①③④

楚汉之争的性质是（）

A . 楚国为反对汉国的侵略而进行的战争 B . 项羽为维护自身的利益而同刘邦进行的战争 C . 刘邦反对项羽大肆杀戮的正义战争 D . 刘邦和项羽为争夺最高统治权而进行的战争

（问题提出）用n个圆最多能把平面分成几个区域？

（问题探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．

探究一：如图1，一个圆能把平面分成2个区域．

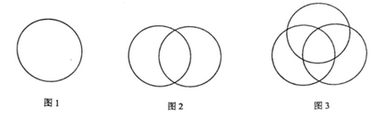
探究二：用2个圆最多能把平面分成几个区域？

如图2，在探究一的基础上，为了使分成的区域最多，应使新增加的圆与前1个圆有2个交点，将新增加的圆分成2部分，从而增加2个区域，所以，用2个圆最多能把平面分成4个区域．

探究三：用3个圆最多能把平面分成几个区域？

如图3，在探究二的基础上，为了使分成的区域最多，应使新增加的圆与前2个圆分别有2个交点，将新增加的圆分成 $\text{[math]}$ 部分，从而增加4个区域，所以，用3个圆最多能把平面分成8个区域．

（1）用4个圆最多能把平面分成几个区域？
仿照前面的探究方法，写出解答过程，不需画图．
（2）（一般结论）用n个圆最多能把平面分成几个区域？
为了使分成的区域最多，应使新增加的圆与前 $\text{[math]}$ 个圆分别有2个交点，将新增加的圆分成部分，从而增加个区域，所以，用n个圆最多能把平面分成个区域．（将结果进行化简）
（3）（结论应用）
①用10个圆最多能把平面分成个区域；

②用个圆最多能把平面分成422个区域．

下列说法正确的是（　）

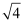A . $\text{[math]}$ 的平方根是±2 B . － $\text{[math]}$ 一定没有算术平方根 C . － $\text{[math]}$ 表示2的算术平方根的相反数 D . 0.9的算术平方根是0.3

如图是种子呼吸作用和植物光合作用的实验装置图，据图回答下列问题：

图片_x0020_1496951865

（1）瓶中加入适量水后种子的呼吸作用会加强，产生的气体增多，从而使玻璃罩内幼苗的光合作用增强，说明此气体是光合作用的
（2）玻璃罩内的绿色植物进行光合作用的主要部位是，所制造的有机物通过（填“导管”或“筛管”）运输到植物体的各个部位。
（3）该装置在光下放置一段时间后，玻璃罩内壁会出现许多水珠，水珠主要来自植物的作用，植物体失水的“门户”是。

They TV at home.

地球最大的生态系统是（）

A . 森林生态系统 B . 学校生态系统 C . 院落生态系统 D . 生物圈

我们通常在晚上六点一刻吃晚饭。

We usually eat dinner at six in the evening.

下列句子没有使用修辞手法的一项是（）

A . 标直漂亮的白桦树在原野上呻吟。 B . 原野到处有一种鸣叫，天空清亮透明，劳动的声音从这头响到那头。 C . 土地是我的母亲，我的每一寸皮肤，都有着土粒。 D . 我想起红布似的高梁，金黄的豆粒，黑色的土地，红玉的脸庞，黑玉的眼睛，斑斓的山雕，奔驰的鹿群，带着松香气味的煤块，带着赤色的足金。

解方程组：